Theoretical probability
Key Notes:
1. Introduction to Probability
- Probability is a measure of how likely an event is to occur.
- It is a way to quantify uncertainty using numbers between 0 (impossible event) and 1 (certain event).
2. Understanding Theoretical Probability
- Theoretical probability is based on mathematical reasoning rather than experiments or observations.
- It calculates the likelihood of an event using the known number of possible outcomes.
3. Formula for Theoretical Probability
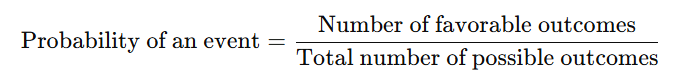
- Favorable outcomes are the specific results we are interested in.
- Total outcomes are all the possible results that could occur.
Learn with an example
📚 You flip a coin.

📚 What is P(heads)?
📚 Write your answer as a percentage. _______%
- Flipping a coin has two possibilities: heads or tails.
- P(heads) =1/2
- Write your answer as a decimal. Then convert your answer to a percentage.
- 1/2 = 0.5 = 50%
- P(heads) = 50%
📚 You pick a card at random.
| 6 | 7 | 8 | 9 |
📚 What is P(6)?
📚 Write your answer as a percentage.______%
- There are 4 cards, numbered 6, 7, 8 and 9.
- P(6) =1/4
- Write your answer as a decimal. Then convert your answer to a percentage.
- 1/4 = 0.25 = 25%
- P(6) = 25%
📚 You roll a 6-sided die.

📚 What is P(factor of 56)?
📚 Simplify your answer and write it as a fraction or whole number._____
- The die has 6 sides, numbered 1, 2, 3, 4, 5 and 6. The factors of 56 are 1, 2 and 4.
- P(factor of 56) =3/6
- Write your answer in simplest form.
- 3/6=1/2
- P(factor of 56) =1/2
Let’s practice!🖊️

