Percent error: area and volume
key notes :
🏫 To find the minimum possible area, subtract the greatest possible error from each measurement before calculating.
🏫 To find the maximum possible area, add the greatest possible error to each measurement before calculating.
Learn with an example
🎯 The rectangle below is labelled with its measured dimensions. Taking measurement error into account, what is the percent error in its calculated area?
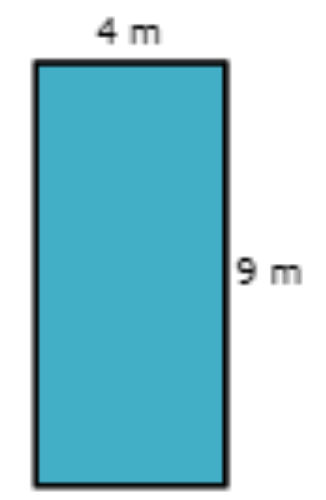
Round your answer to the nearest tenth of a percent and include a percent sign (%).
You want to find the percent error in area, taking measurement error into account.
Step 1: Find the measured area.
To find the measured area, multiply the measured dimensions.
Ameas = LmeasWmeas
= (4)(9)
= 36
Step 2: Find the minimum possible area and the maximum possible area.
First find the greatest possible error. Each measurement was made to the nearest whole metre, so the greatest possible error is half of 1 metre, which is 0.5 metres.
To find the maximum possible area, add the greatest possible error to each measurement, then multiply.
Amax = LmaxWmax
= (4 + 0.5)(9 + 0.5)Addthegreatestpossibleerror,0.5
= (4.5)(9.5)
= 42.75
To find the minimum possible area, subtract the greatest possible error from each measurement, then multiply.
Amin = LminWmin
= (4 − 0.5)(9 − 0.5)Subtractthegreatestpossibleerror,0.5
= (3.5)(8.5)
= 29.75
Step 3: Find the greater difference in area.
Calculate the difference between the minimum area and the measured area, and between the maximum area and the measured area. The larger difference will be the greatest possible error in area.
Difference using minimum area:
| Ameas − Amin | = | 36 − 29.75 = 6.25 |
Difference using maximum area:
| Amax − Ameas | = | 42.75 − 36 = 6.75 |
- The second difference is larger. So, the greatest possible error in area is 6.75.
Step 4: Calculate the percent error in the area.
| percent error in area | = | greatest possible error in areameasured area | |
| = | 6.7536 | ||
| = | 0.1875 |
Write the number as a percent.
0.1875 → 18.75%
Round to the nearest tenth of a percent.
18.75% → 18.8%
To the nearest tenth of a percent, the percent error is 18.8%.
🎯 The rectangle below is labelled with its measured dimensions. Taking measurement error into account, what is the percent error in its calculated area?
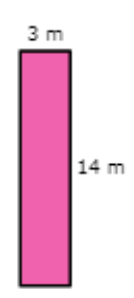
You want to find the percent error in area, taking measurement error into account.
Step 1: Find the measured area.
To find the measured area, multiply the measured dimensions.
Ameas = LmeasWmeas
= (3)(14)
= 42
Step 2: Find the minimum possible area and the maximum possible area.
First find the greatest possible error. Each measurement was made to the nearest whole metre, so the greatest possible error is half of 1 metre, which is 0.5 metres.
To find the maximum possible area, add the greatest possible error to each measurement, then multiply.
Amax = LmaxWmax
= (3 + 0.5)(14 + 0.5)Addthegreatestpossibleerror,0.5
= (3.5)(14.5)
= 50.75
To find the minimum possible area, subtract the greatest possible error from each measurement, then multiply.
Amin = LminWmin
= (3 − 0.5)(14 − 0.5)Subtractthegreatestpossibleerror,0.5
= (2.5)(13.5)
= 33.75
Step 3: Find the greater difference in area.
Calculate the difference between the minimum area and the measured area, and between the maximum area and the measured area. The larger difference will be the greatest possible error in area.
Difference using minimum area:
| Ameas − Amin | = | 42 − 33.75 = 8.25 |
Difference using maximum area:
| Amax − Ameas | = | 50.75 − 42 = 8.75 |
- The second difference is larger. So, the greatest possible error in area is 8.75.
Step 4: Calculate the percent error in the area.
| percent error in area | = | greatest possible error in areameasured area | |
| = | 8.7542 | ||
| ≈ | 0.20833 |
Write the number as a percent.
0.20833 → 20.833%
Round to the nearest tenth of a percent.
20.833% → 20.8%
To the nearest tenth of a percent, the percent error is 20.8%.
🎯 The rectangle below is labelled with its measured dimensions. Taking measurement error into account, what is the percent error in its calculated area?
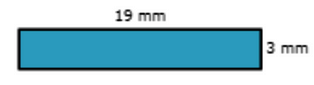
You want to find the percent error in area, taking measurement error into account.
Step 1: Find the measured area.
To find the measured area, multiply the measured dimensions.
Ameas = LmeasWmeas
= (19)(3)
= 57
Step 2: Find the minimum possible area and the maximum possible area.
First find the greatest possible error. Each measurement was made to the nearest whole millimetre, so the greatest possible error is half of 1 millimetre, which is 0.5 millimetres.
To find the maximum possible area, add the greatest possible error to each measurement, then multiply.
Amax = LmaxWmax
= (19 + 0.5)(3 + 0.5)Addthegreatestpossibleerror,0.5
= (19.5)(3.5)
= 68.25
To find the minimum possible area, subtract the greatest possible error from each measurement, then multiply.
Amin = LminWmin
= (19 − 0.5)(3 − 0.5)Subtractthegreatestpossibleerror,0.5
= (18.5)(2.5)
= 46.25
Step 3: Find the greater difference in area.
Calculate the difference between the minimum area and the measured area, and between the maximum area and the measured area. The larger difference will be the greatest possible error in area.
Difference using minimum area:
| Ameas − Amin | = | 57 − 46.25 = 10.75 |
Difference using maximum area:
| Amax − Ameas | = | 68.25 − 57 = 11.25 |
- The second difference is larger. So, the greatest possible error in area is 11.25.
Step 4: Calculate the percent error in the area.
| percent error in area | = | greatest possible error in areameasured area | |
| = | 11.2557 | ||
| ≈ | 0.19737 |
Write the number as a percent.
0.19737 → 19.737%
Round to the nearest tenth of a percent.
19.737% → 19.7%
To the nearest tenth of a percent, the percent error is 19.7%.
Let’s practice!🖊️

