Surface area and volume review
key notes :
Surface Area
Surface area is the total area of all the faces of a three-dimensional shape.
It is measured in square units (e.g., cm², m²).
Formulas for Surface Area:
- Cube: 6s2 (where sss is the side length)
- Rectangular Prism: 2(lw+lh+wh) (where l,w,h are length, width, and height)
- Sphere: 4πr2 (where r is the radius)
- Cylinder: 2πr2+2πrh (where r is radius, h is height)
- Cone: πr2+πrl (where r is radius, l is slant height)
- Pyramid: B+1/2Pl (where B is the base area, P is the perimeter of the base, and l is slant height)
Volume
Volume is the amount of space occupied by a three-dimensional object.
It is measured in cubic units (e.g., cm³, m³).
Formulas for Volume:
- Cube: s3
- Rectangular Prism: lwh
- Sphere: 4/3πr3
- Cylinder: πr2h
- Cone: 1/3 πr2h
- Pyramid: 1/3 Bh
Relationship Between Surface Area and Volume
- Surface area affects how fast an object exchanges heat or dissolves.
- Volume determines the capacity of an object.
- As an object increases in size, volume grows faster than surface area.
Problem-Solving Tips
Identify the shape and use the correct formula.
Ensure correct unit conversions (e.g., cm² to m², cm³ to liters).
Break complex shapes into simpler parts.
Use π ≈ 3.14 when necessary.
Check if the problem requires total or lateral surface area.
Learn with an example
📚 What is the surface area of this sphere?
📚 Use 𝜋 ≈ 3.14 and round your answer to the nearest hundredth.
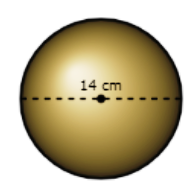
_______square centimetres
- Find the radius of the sphere.radius =
| 12 × diameter | = | 12 × 14 = 7 |
- Use this number in the surface area formula. Use 𝜋 ≈ 3.14.
- Surface area = 4𝜋r2
- ≈ 4 × 3.14 × 72
- ≈ 615.44The surface area of the sphere is about 615.44 square centimetres.
📚 What is the volume?
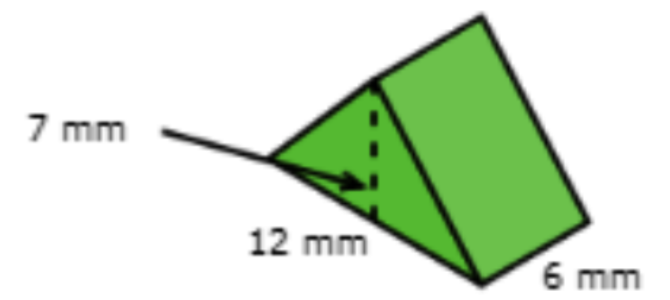
________ cubic millimetres.
- Find the base, height, and length of the triangular prism.
- base: 12 mm
height: 7 mm
length: 6 mm
Use these numbers in the volume formula.
| Volume | = | 12 × base × height × length |
| = | 12 × 12 × 7 × 6 | |
| = | 252 |
- The volume is 252 cubic millimetres.
📚 The surface area of this cone is 414.48 square millimetres. What is the slant height of this cone?
📚 Use 𝜋 ≈ 3.14 and round your answer to the nearest hundredth.
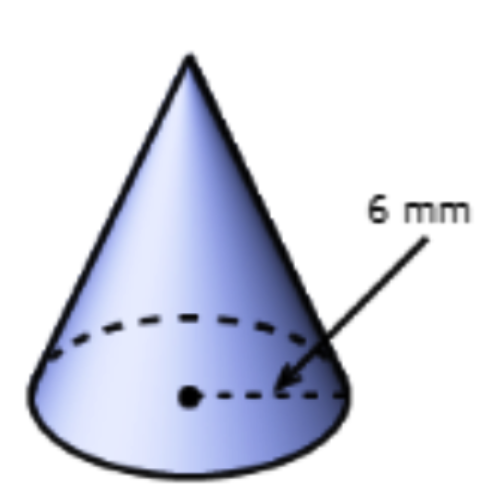
s ≈ _______ millimetres
- Find the surface area and radius of the cone.
surface area = 414.48
radius = 6
Find the area of the base. Use 𝜋 ≈ 3.14.
Area of base = 𝜋r2
≈ 3.14 × 62
≈ 113.04 - Find the lateral area.
Lateral area = 𝜋rs
≈ 3.14 × 6 × s
≈ 18.84s - Now add the areas to find the slant height of the cone.
| Surface area | = | B + L.A. |
| 414.48 | ≈ | 113.04 + 18.84s |
| 414.48 − 113.04 | ≈ | 18.84s |
| 301.44 | ≈ | 18.84s |
| 301.44 ÷ 18.84 | ≈ | s |
| 16 | ≈ | s |
- The slant height of the cone is about 16 millimetres.
Let’s practice!

