Surface area and volume of similar solids
key notes :
Definition of Similar Solids
- Two solids are similar if they have the same shape but different sizes.
- Corresponding angles are equal, and corresponding sides are proportional.
Scale Factor (k)
- The scale factor is the ratio of corresponding linear dimensions (lengths, widths, or heights) of two similar solids.
- If the scale factor between two similar solids is k, then all corresponding linear measurements (edges, radii, heights) are in the ratio 1:k.
Surface Area Ratio
- The ratio of the surface areas of two similar solids is the square of the scale factor.
- Formula:
Surface Area of Solid 1 / Surface Area of Solid 2 = k2
- If the scale factor is k, then:
Surface Area of larger solid = k2 × Surface Area of smaller solid
Volume Ratio
- The ratio of the volumes of two similar solids is the cube of the scale factor.
- Formula:
Volume of Solid 1 / Volume of Solid 2 = k3
- If the scale factor is k, then:
Volume of larger solid = k3 × Volume of smaller solid
Example Calculation
If two similar spheres have a scale factor of 2, then:
- Their surface area ratio is 22 = 4.
- Their volume ratio is 23 = 8.
Key Formulas Summary
Scale Factor (k): Ratio of corresponding lengths.
Surface Area Ratio: k2.
Volume Ratio: k3.
Learn with an example
The figures below are similar.
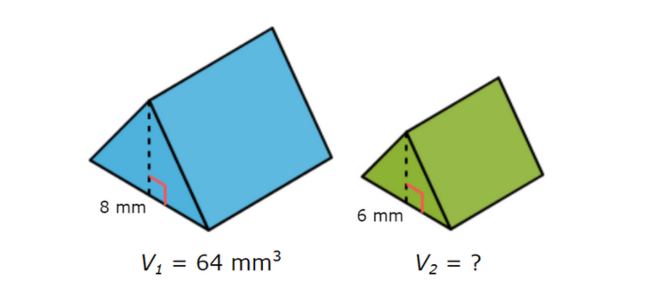
What is the volume of the smaller triangular prism?
V2 = _____ cubic millimetres
Find the cube of the ratio of the corresponding dimensions:
(a/v)3 = (8/6)3 = (4/3)3 = 64/27
Find the ratio of the volumes:
V1/V2 = 64/V2
Use these two ratios to set up a proportion and solve for V2.
64/27 = 64/V2
64/27 ( 27V2 ) = 64/V2 ( 27V2 ) Multiply both sides by 27V2
64V2 = 64 · 27 Simplify
64V2 = 1,728 Simplify
64V2÷ 64 = 1,728 ÷ 64 Divide both sides by 64
V2= 27
The volume of the smaller triangular prism is 27 cubic millimetres.
The figures below are similar.
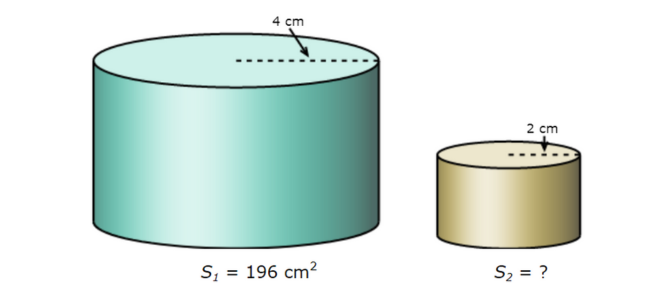
What is the surface area of the smaller cylinder?
S2 = _______ square centimetres
Find the square of the ratio of the corresponding dimensions:
(a/b)2 = (4/2)2 = (2/1)1 = 4/1
Find the ratio of the surface areas:
S1/S2 = 196/S2
Use these two ratios to set up a proportion and solve for S2.
4/1 = 196/S2
4/1 ( S2 ) = 196/S2 ( S2 )
4S2=196 · 1 Simplify
4S2= 196 Simplify
4S2÷ 4=196 ÷ 4 Divide both sides by 4
S2= 49
The surface area of the smaller cylinder is 49 square centimetres.
Let’s practice!

