Introduction to similar solids
key notes :
Definition of Similar Solids
- Two solids are similar if their corresponding dimensions are proportional and their corresponding angles are equal.
Properties of Similar Solids
- Same shape but different sizes
- Corresponding linear dimensions are proportional
- Corresponding angles remain the same
Scale Factor
- The ratio of corresponding linear dimensions (e.g., heights, radii, or side lengths) of two similar solids.
Ratios of Measurements
- Length Ratio: If the scale factor between two similar solids is k, then all corresponding lengths have a ratio of k.
- Surface Area Ratio: The ratio of surface areas is k2.
- Volume Ratio: The ratio of volumes is k3.
Examples of Similar Solids
- Similar cubes, spheres, cones, cylinders, and pyramids.
- Enlarged or reduced 3D models in architecture and engineering.
Real-World Applications
- Model-making in architecture and design.
- Scaling up or down objects in engineering and manufacturing.
- Understanding relationships in nature (e.g., large and small planets).
How to Determine if Two Solids are Similar
Compare corresponding linear dimensions to see if they have a constant ratio.
Check if angles remain the same in corresponding parts of the solids.
Verify surface area and volume ratios using the scale factor.
Learn with an example
The figures below are similar. What is a?
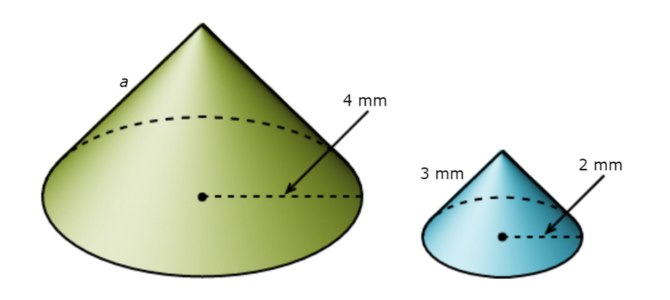
a = ________millimetres
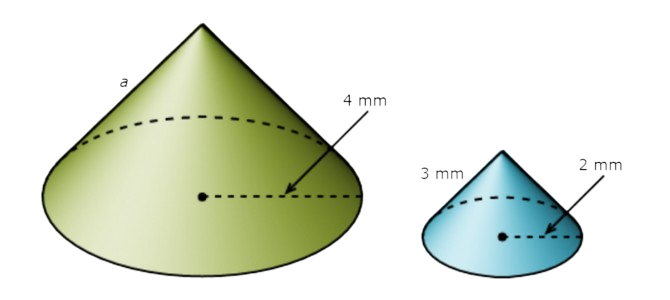
Look at the similar figures and find two pairs of corresponding lengths. One pair of corresponding lengths is 2 mm and 4 mm. Another pair of corresponding lengths is 3 mm and a.
Use these two pairs of corresponding lengths to set up a proportion and solve for a.
2/4 = 3/a Plug in the pairs of corresponding lengths
2/4 (4 · a) = 3/a (4.a) Multiply both sides by (4 · a)
2 a=3 · 4 Simplify
2 a= 12 Simplify
2 a ÷ 2=12 ÷ 2 Divide both sides by 2
a = 6
The missing length is 6 millimetres.
The figures below are similar. What is b?
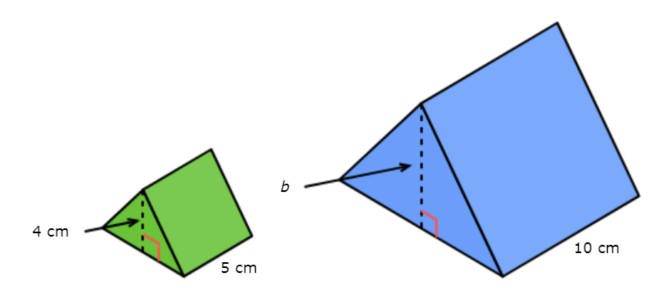
b =______ centimetres
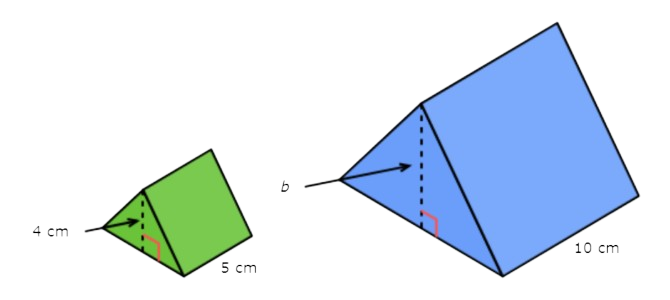
Look at the similar figures and find two pairs of corresponding lengths. One pair of corresponding lengths is 5 cm and 10 cm. Another pair of corresponding lengths is 4 cm and b.
Use these two pairs of corresponding lengths to set up a proportion and solve for b.
5/10 = 4/b Plug in the pairs of corresponding lengths
5/10 ( 10.b ) = 4/b ( 10.b ) Multiply both sides by (10 · b)
5b =4 · 10 Simplify
5b= 40 Simplify
5b÷ 5 = 40 ÷ 5 Divide both sides by 5
b = 8
The missing length is 8 centimetres.
The figures below are similar. What is q?
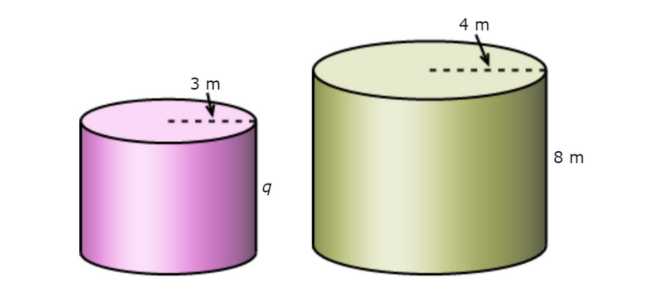
q =_______metres
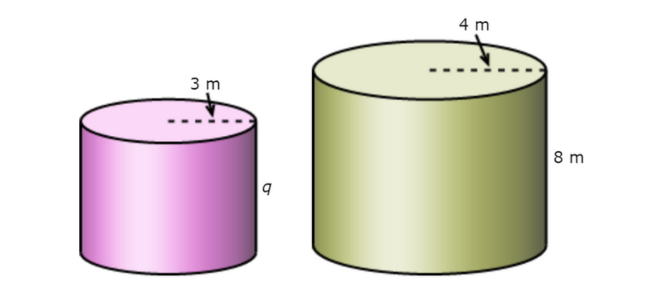
Look at the similar figures and find two pairs of corresponding lengths. One pair of corresponding lengths is 4 m and 3 m. Another pair of corresponding lengths is 8 m and q.
Use these two pairs of corresponding lengths to set up a proportion and solve for q.
4/3 = 8/q Plug in the pairs of corresponding lengths
4/3 ( 3.a ) = 8/q ( 3.q ) Multiply both sides by (3 · q)
4q=8 · 3 Simplify
4q= 24 Simplify
4q÷ 4=24 ÷ 4 Divide both sides by 4
q = 6
The missing length is 6 metres.
Let’s practice!

