Volume of prisms and cylinders
key notes :
Definition of Volume
- Volume is the amount of space occupied by a 3D object.
- It is measured in cubic units (e.g., cm³, m³).
Volume of a Prism
- A prism is a solid with two identical bases and rectangular lateral faces.
- Formula:
V = B × h
where:
B = Area of the base
h = Height of the prism
Types of Prisms:
Rectangular Prism: V = l × w × h
Triangular Prism: V = 12 × b × hbase × hprism
Volume of a Cylinder
A cylinder is a 3D shape with two circular bases and a curved surface.
Formula:
V = πr2h
where:
r = Radius of the circular base
h = Height of the cylinder
π ≈ 3.1416
Comparing Prisms and Cylinders
- Both follow the general volume formula: Base Area × Height
- A prism has polygonal bases, while a cylinder has circular bases.
Key Problem-Solving Steps
- Identify the shape (prism or cylinder).
- Find the base area (BBB) using appropriate formulas.
- Multiply the base area by the height (hhh).
- Use proper units and round off answers if necessary.
Example Problems
Find the volume of a rectangular prism with dimensions 5 cm × 4 cm × 10 cm.
V = 5 × 4 × 10 = 200 cm3
Calculate the volume of a cylinder with radius 7 cm and height 12 cm.
V = π (72)(12) = π(49)(12) = 588π ≈ 1847.52 cm3
Learn with an example
What is the volume?
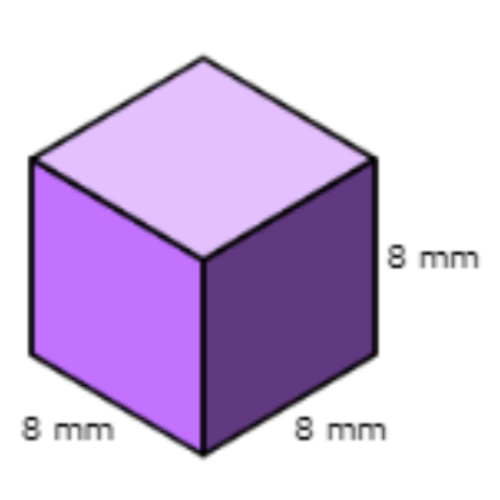
_______ cubic millimetres.
Each side of the cube is 8 millimetres long. Use the number 8 in the formula.
volume=side . side . side
= 8 . 8 . 8
= 512
The volume is 512 cubic millimetres.
What is the volume of this cylinder?
Use 𝜋 ≈ 3.14 and round your answer to the nearest hundredth.
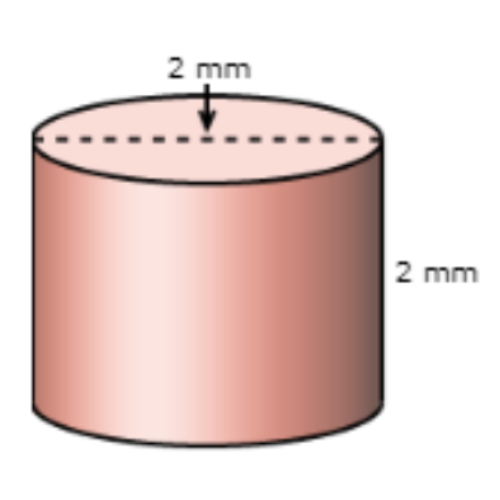
______ cubic millimetres.
Find the radius and height of the cylinder.
radius = 1/2 . diameter=1/2 . 2 = 1
height = 2
Use these numbers in the volume formula. Use 3.14 for 𝜋.
volume = 𝜋r2 h
≈ 3.14 . 1 . 1 . 2
≈ 6.28
The volume of the cylinder is about 6.28 cubic millimetres.
What is the volume of this cylinder?
Use 𝜋 ≈ 3.14 and round your answer to the nearest hundredth.
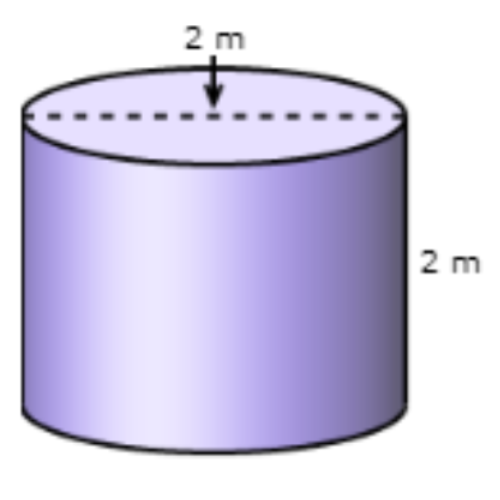
_______ cubic millimetres.
Find the radius and height of the cylinder.
radius = 1/2 . diameter =1/2 . 2 = 1
height = 2
Use these numbers in the volume formula. Use 3.14 for 𝜋.
volume = 𝜋r2 h
≈ 3.14 . 1 . 1 . 2
≈ 6.28
The volume of the cylinder is about 6.28 cubic millimetres.
let’s practice!

