Solve a right triangle
key notes :
The sine (sin) of an angle in a right triangle is a ratio. It is the length of the opposite leg (opp) divided by the length of the hypotenuse (hyp). The opposite leg is the side across from the specified angle and the hypotenuse is the side across from the right angle.
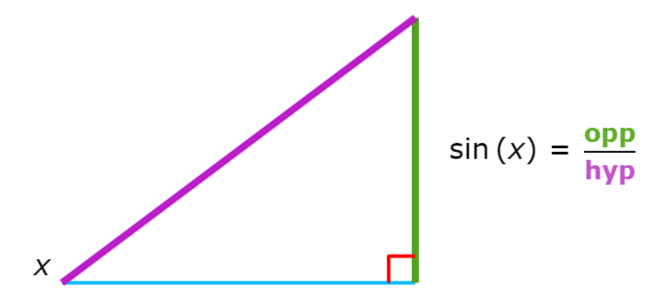
Learn with an example
Solve the right triangle.
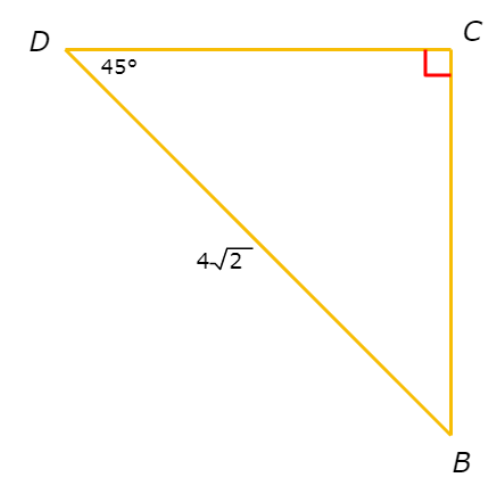
Write your answers in simplified, rationalised form. Do not round.
BC =
CD =
∠B =______°
Find sin45°.
To calculate sin45°, first draw the 45°-45°-90° special right triangle.
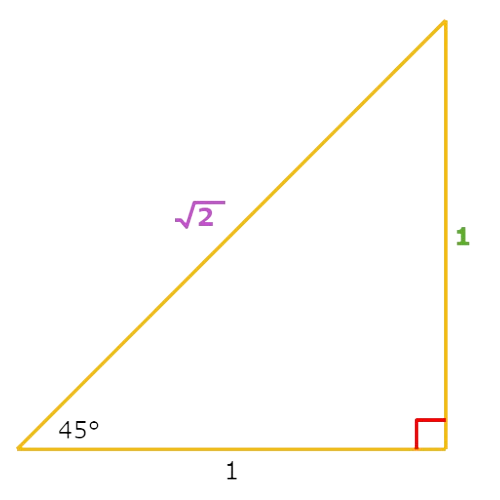
Calculate sin 45°.
sin 45° = opp/hyp Definition of sine
= 1/√2 Plug in opp=1 and hyp= √2
= 1/√2 . √2/√2 Rationalise the denominator
= √2/2 Multiply
So, sin4 5°= √2/2 .
Find BC.
Use the definition of sine (sin) to write an equation, then solve for BC.
sin 45° = BC / 4√2 Given
√2/2 = BC / 4√2 Substitute sin 45°= √2/2
4√2 . √2/2 = BC Multiply both sides by 4√2
4 = BC Simplify
So, BC=4.
Find CD.
Use Pythagoras’ theorem to find CD.
CD2+BC2= BD2 Pythagoras’ Theorem
CD2+42= (4√2)2 Plug in BC=4 and BD=4√2
CD2+16= 32 Square
CD2= 16 Subtract 16 from both sides
CD= 4 Take the square root of both sides
So, CD=4.
Find ∠B.
∠B and ∠D are the acute angles of a right triangle, so they are complementary. Write an equation setting the sum of their measures equal to 90°, and solve for ∠B.
∠B+∠D= 90°
∠B+45° = 90° Plug in ∠D=45°
∠B = 45° Subtract 45° from both sides
So, ∠B=45°.
To summarize, BC=4, CD=4 and ∠B=45°.
Solve the right triangle.

Write your answers in simplified, rationalised form. Do not round.
GH =
FH =
∠G =______°
Find sin60°.
To calculate sin60°, first draw the 30°-60°-90° special right triangle.
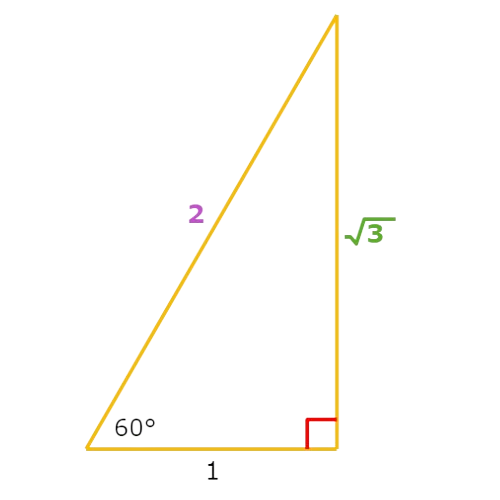
Calculate sin60°.
sin60° = opp/hyp Definition of sine
= √3/2 Plug in opp=√3 and hyp=2
So, sin60°=√3/2 .
Find GH.
Use the definition of sine (sin) to write an equation, then solve for GH.
sin60° = GH/6 Given
√3/2 = GH/6 Substitute sin60°=√3/2
6 . √3/2 = GH Multiply both sides by 6
3√3= GH Simplify
So, GH = 3√3.
Find FH.
Use Pythagoras’ theorem to find FH.
FH2+GH2 = FG2 Pythagoras’ Theorem
FH2+(3√32)= 62 Plug in GH=3√3 and FG=6
FH2+27= 36 Square
FH2 = 9 Subtract 27 from both sides
FH= 3 Take the square root of both sides
So, FH=3.
Find ∠G.
∠F and ∠G are the acute angles of a right triangle, so they are complementary. Write an equation setting the sum of their measures equal to 90°, and solve for ∠G.
∠F+∠G= 90°
60°+∠G= 90° Plug in ∠F=60°
∠G= 30° Subtract 60° from both sides
So, ∠G=30°.
To summarize, GH=3√3, FH=3 and ∠G=30°.
let’s practice!

