Trigonometric ratios: find an angle measure
key notes :
The sine (sin) of an angle in a right triangle is a ratio. It is the length of the opposite leg (opp) divided by the length of the hypotenuse (hyp). The opposite leg is the side across from the specified angle and the hypotenuse is the side across from the right angle.
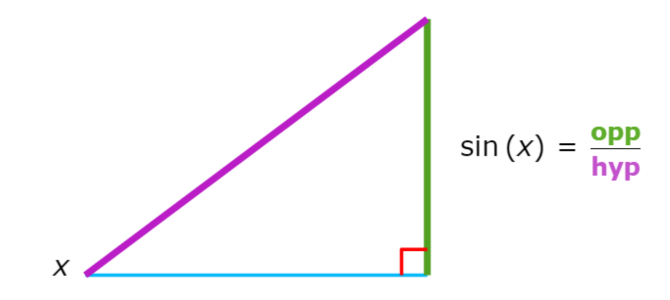
Learn with an example
Find ∠J.
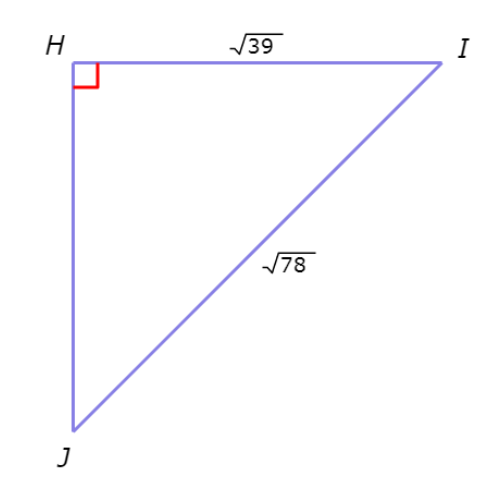
∠J =_______°
Find sin(J).
Find the sine (sin) of ∠J.
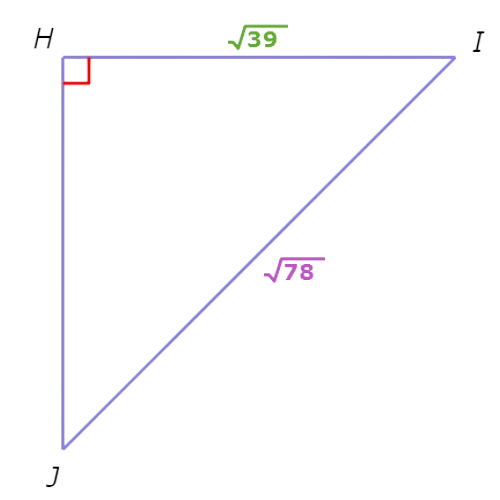
sin(J) = opp / hyp Definition of sine
HI / IJ Substitute opp=HI and hyp=IJ
= √39/√78 Plug in HI= √39 and IJ= √78
= √39/√78 . √78/√78 Rationalise the denominator
= 39 2 / 78 Multiply
= √2/2 Simplify
So, sin(J)= √2/2 .
Find ∠J.
If you remember that sin45°= √2/2 , then you know that ∠J=45°.
Find ∠G.
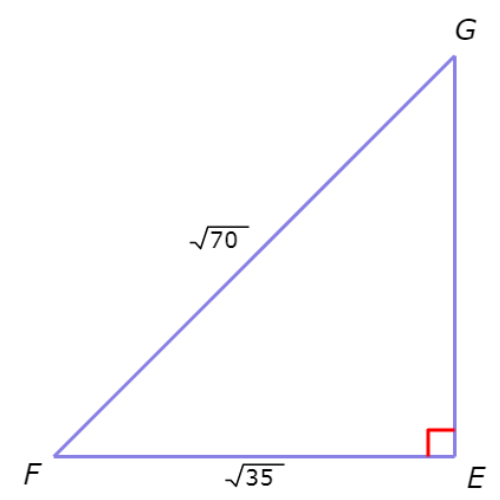
∠G =________°
Find sin(G).
Find the sine (sin) of ∠G.
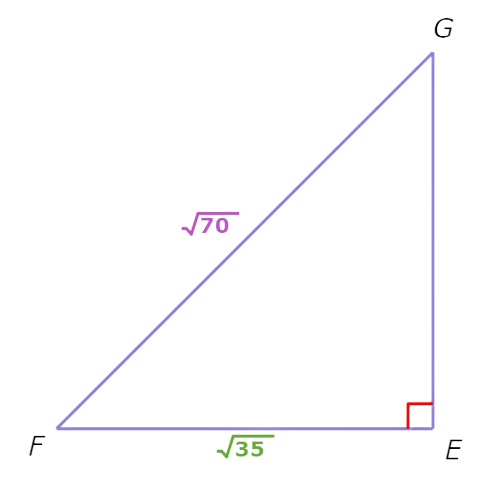
sin(G) = opp / hyp Definition of sine
= EF / FG Substitute opp=EF and hyp=FG
= 35/70 Plug in EF=√35 and FG= √70
= √35/√70 . √70/√70 Rationalise the denominator
= 35√2 / 70 Multiply
= √2/2 Simplify
So, sin(G)= √2/2 .
Find ∠G.
If you remember that sin45°= √2/2 , then you know that ∠G=45°.
let’s practice!

