Inverses of trigonometric functions
key notes :
The cosine (cos) of an angle in a right triangle is a ratio. It is the length of the adjacent leg (adj) divided by the length of the hypotenuse (hyp). The adjacent leg is the leg next to the specified angle and the hypotenuse is the side across from the right angle.

Learn with an example
x is an acute angle. Find the value of x in degrees.
cos (x) = 1/2
x= _______°
You are looking for an exact answer, so see if 1/2 is the cosine (cos) of an angle from a 30°-60°-90° special triangle or a 45°-45°-90° special triangle.
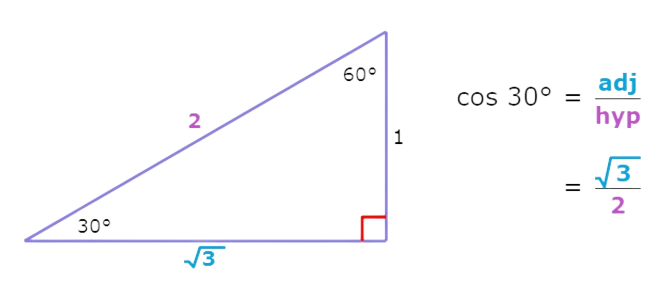
You can use the definition of cosine and the following reference triangles to calculate the cosines of 30°, 45° and 60°.
Find cos30°.
Find cos 45°.

Find cos60°.

Since cos(x)= 1/2 , x=60°.
x is an acute angle. Find the value of x in degrees.
cos(x) = √2/2 .
x=____°
You are looking for an exact answer, so see if √2/2 . is the cosine (cos) of an angle from a 30°-60°-90° special triangle or a 45°-45°-90° special triangle.
You can use the definition of cosine and the following reference triangles to calculate the cosines of 30°, 45° and 60°.
Find cos30°.

Find cos45°.

Find cos60°.

Since cos(x)= √2/2 , x=45°.
let’s practice!

