Introduction

• Proposed by Arnold Sommerfeld in 1916 as an extension of Bohr’s Model of the atom.

• Addressed the limitations of Bohr’s model by introducing elliptical orbits in addition to circular ones.
• Explained fine structure (splitting) of spectral lines observed in atoms like hydrogen.

Key Features of Bohr-Sommerfeld Model

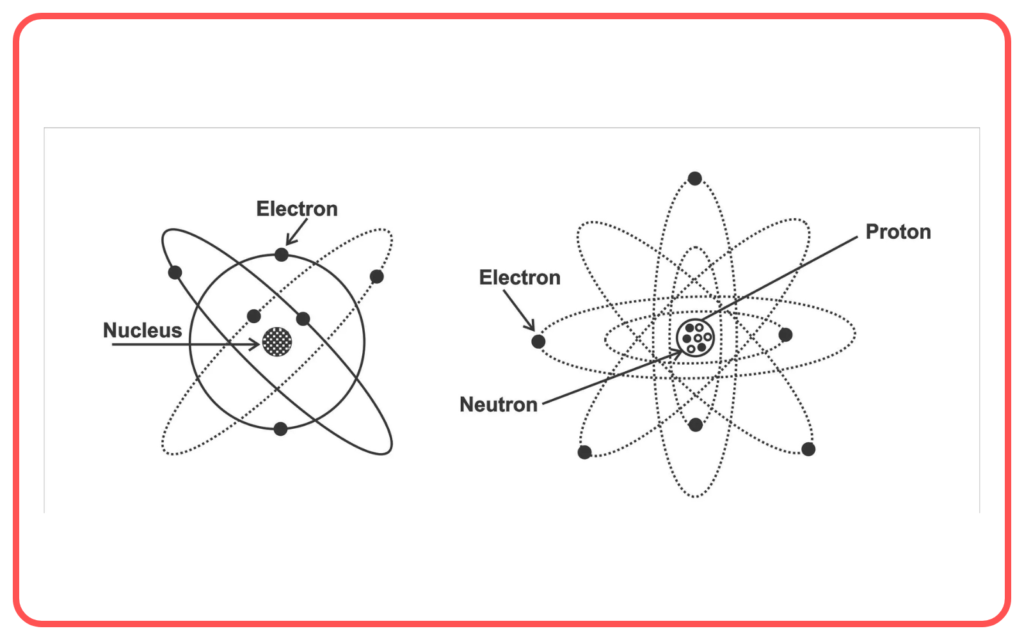
• Elliptical Orbits
  • Electrons can move in both circular and elliptical orbits around the nucleus.
  • The nucleus is located at one of the focal points of the ellipse.

• Two Quantum Numbers
  • Introduced two quantum numbers to describe electron motion:
    1. Principal Quantum Number (n): Determines the size and energy of the orbit.Azimuthal Quantum Number (k): Determines the shape of the orbit.
    • k ranges from 1 to n and defines how elliptical the orbit is.

• Orbital Energy and Angular Momentum
  • The total energy of the electron depends on its principal quantum number (n), similar to Bohr’s model.
  • The angular momentum of an electron in elliptical orbits is quantized: L=kh/2π,k≤n
• Relativistic Effects
  • Sommerfeld introduced relativistic corrections for high-speed electrons in inner orbits, which improved the accuracy of predictions for spectral lines.

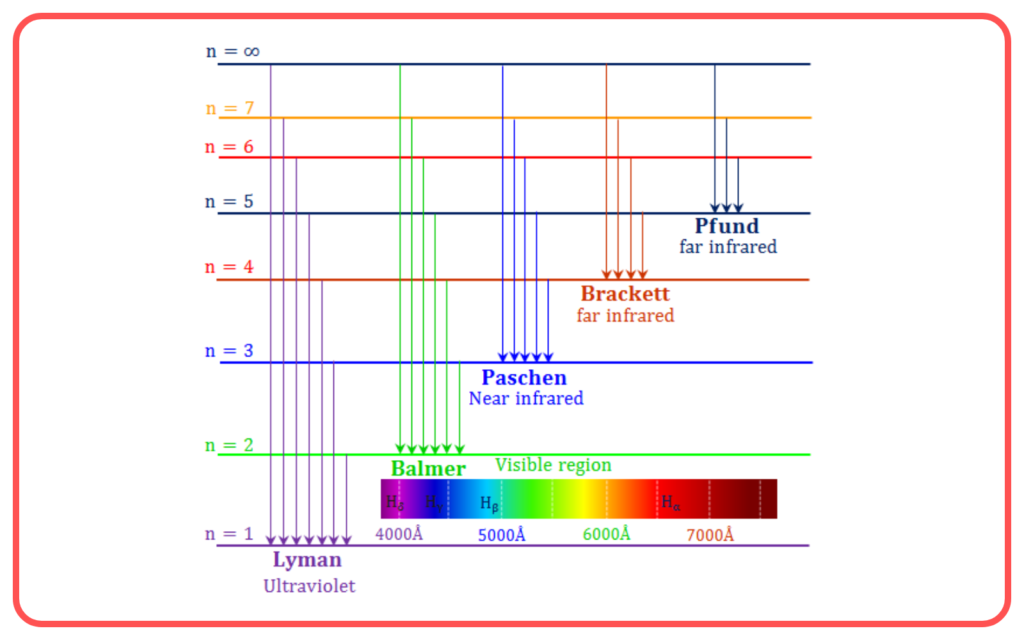
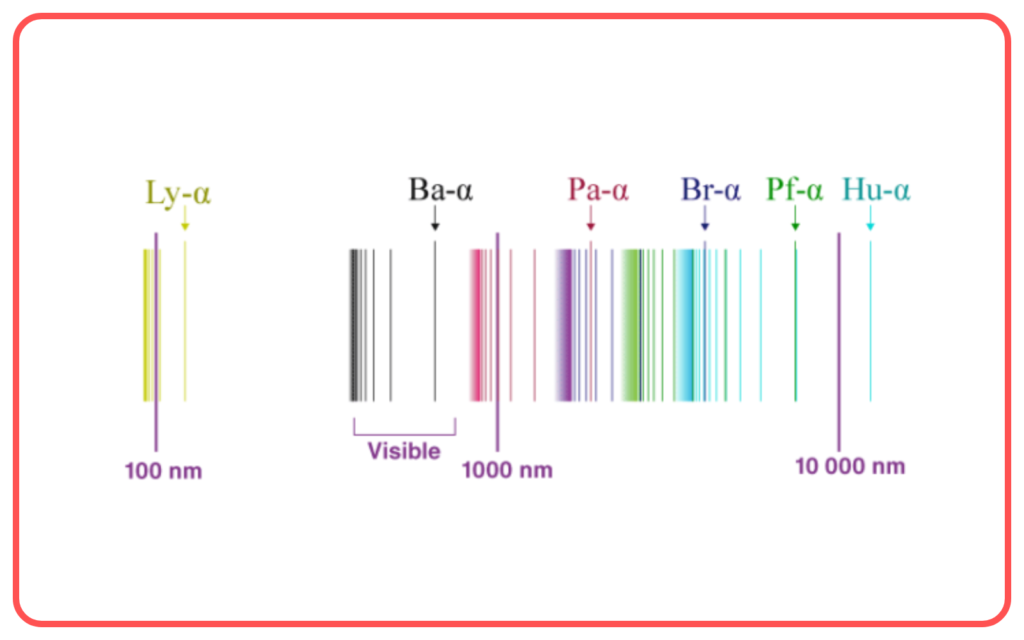
Fine Structure of Spectral Lines

• The model explained the splitting of spectral lines into closely spaced components due to the different shapes (elliptical and circular) of orbits.
• Provided a better understanding of the hydrogen spectrum compared to Bohr’s model.

Achievements of the Bohr-Sommerfeld Model

• Extended Bohr’s theory to explain fine structure in spectral lines.

• Incorporated elliptical orbits, making the model more realistic.
• Introduced additional quantum numbers, paving the way for quantum mechanics.

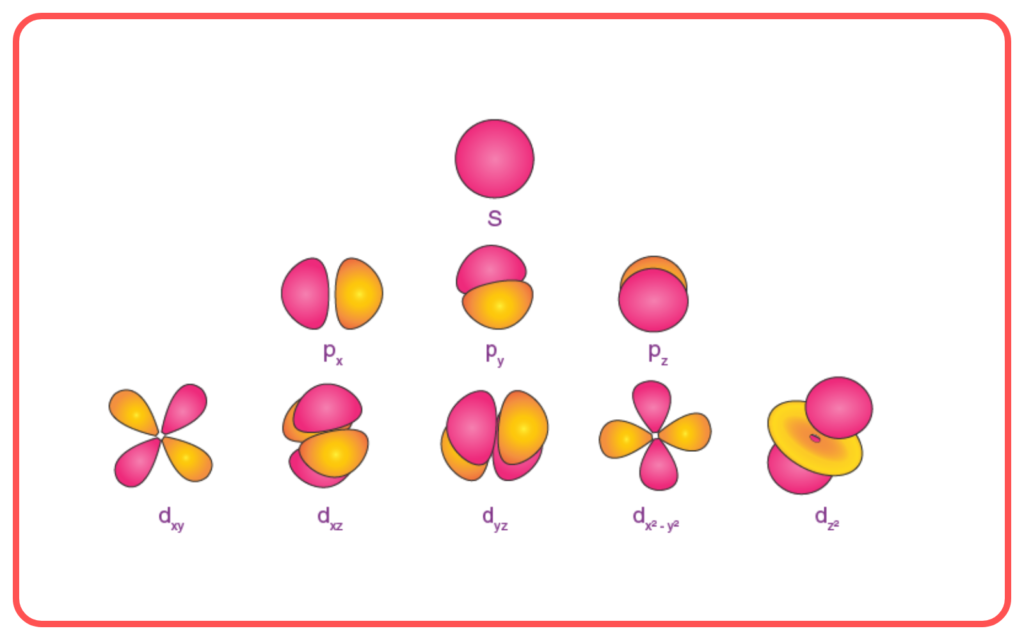
Limitations of the Bohr-Sommerfeld Model

• Applicable Only to Hydrogen-like Atoms
  • Could not accurately explain spectra of multi-electron atoms.
• Failed to Explain Zeeman Effect
  • Could not completely explain the splitting of spectral lines in magnetic fields.

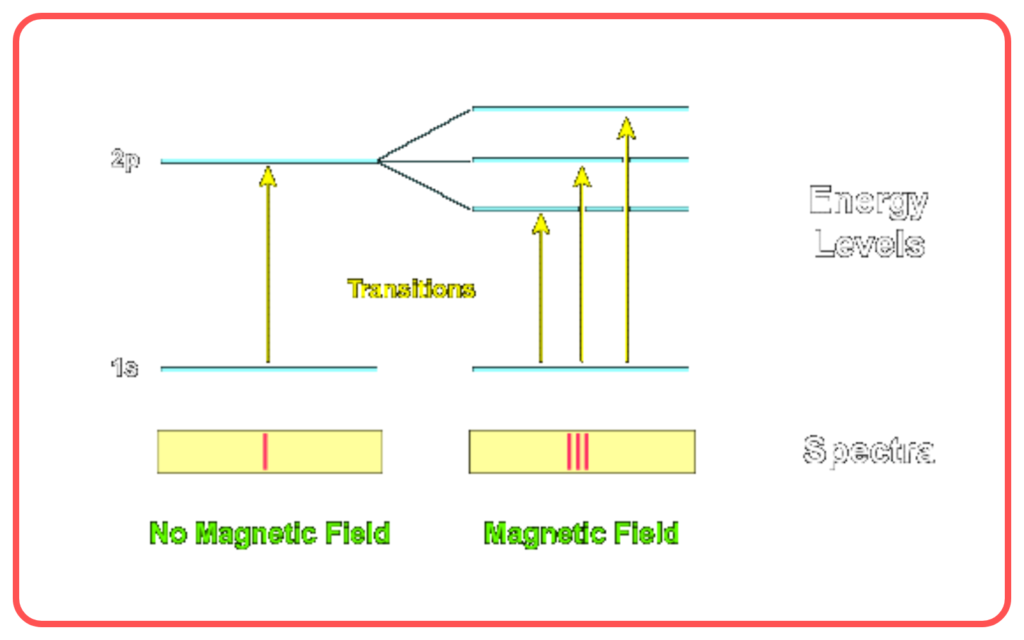
• Incompatibility with Wave-Particle Duality
  • Did not incorporate the wave-like behavior of electrons (proposed later by de Broglie).
• Violation of Heisenberg’s Uncertainty Principle
  • Assumed well-defined paths for electrons, which contradicts quantum mechanics.
• Superseded by Quantum Mechanical Model
  • Could not explain finer details of atomic structure, which were addressed by the Schrödinger wave equation.

Comparison with Bohr’s Model

Feature	Bohr’s Model	Bohr-Sommerfeld Model
Shape of Orbits	Circular only	Circular and elliptical
Quantum Numbers	Principal (n) only	Principal (n) and azimuthal (k)
Spectral Line Explanation	Broad hydrogen spectrum	Fine structure of hydrogen spectrum
Relativity	Not included	Included

---

Conclusion

• The Bohr-Sommerfeld Model was an important step in refining atomic theory and bridging the gap between Bohr’s atomic model and the modern quantum mechanical model.
• It introduced critical concepts like elliptical orbits and quantum numbers that are foundational in understanding atomic behavior.

Let’s practice