• A current-carrying conductor placed in a magnetic field experiences a force.

• This happens because the magnetic field exerts a force on the moving charges (electrons) in the conductor.

Factors Affecting the Force

The magnitude of the force depends on:

1. Magnetic Field Strength (B) – Stronger the field, greater the force.
2. Current in the Conductor (I) – More current increases the force.
3. Length of the Conductor (L) – Longer the conductor, greater the force.
4. Angle (θ) – The angle between the current direction and magnetic field.

Formula for Force

The magnitude of the force is calculated using the formula: F=BILsin⁡θF

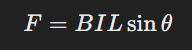
Where:

• F = Force (in Newtons, N)
• B = Magnetic field strength (in Tesla, T)
• I = Current (in Amperes, A)
• L = Length of the conductor (in meters, m)
• θ= Angle between the current and the magnetic field.

---

Special Cases

• Maximum Force: When 𝜃 = 90°(current is perpendicular to the magnetic field)

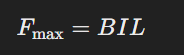
• Zero Force: When 𝜃 = 0° or 180°(current is parallel or anti−parallel to the magnetic field)

---

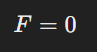
Direction of the Force

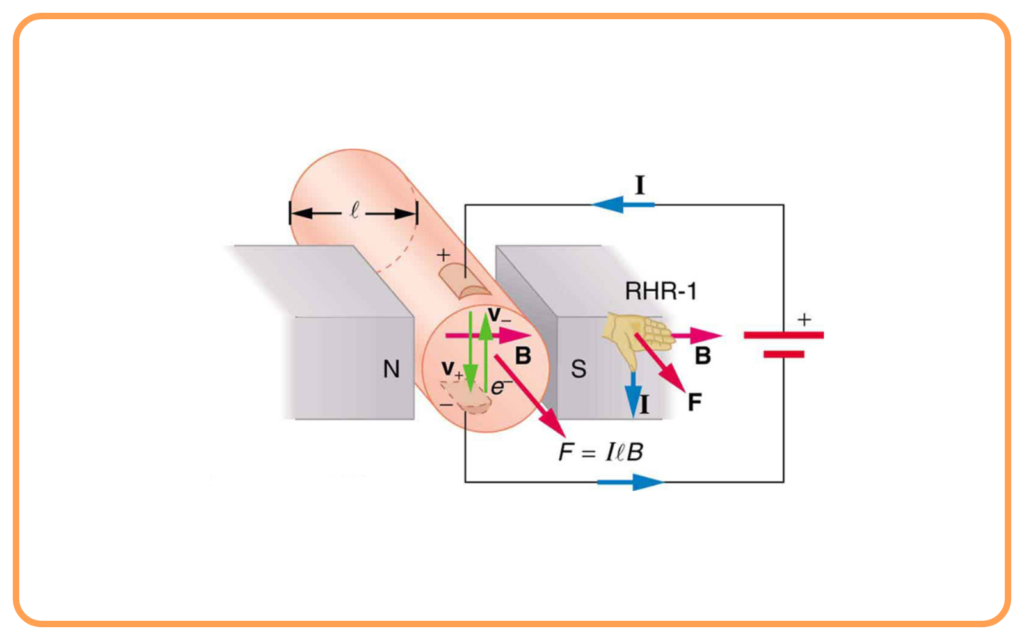
The direction of the force is determined by Fleming’s Left-Hand Rule:

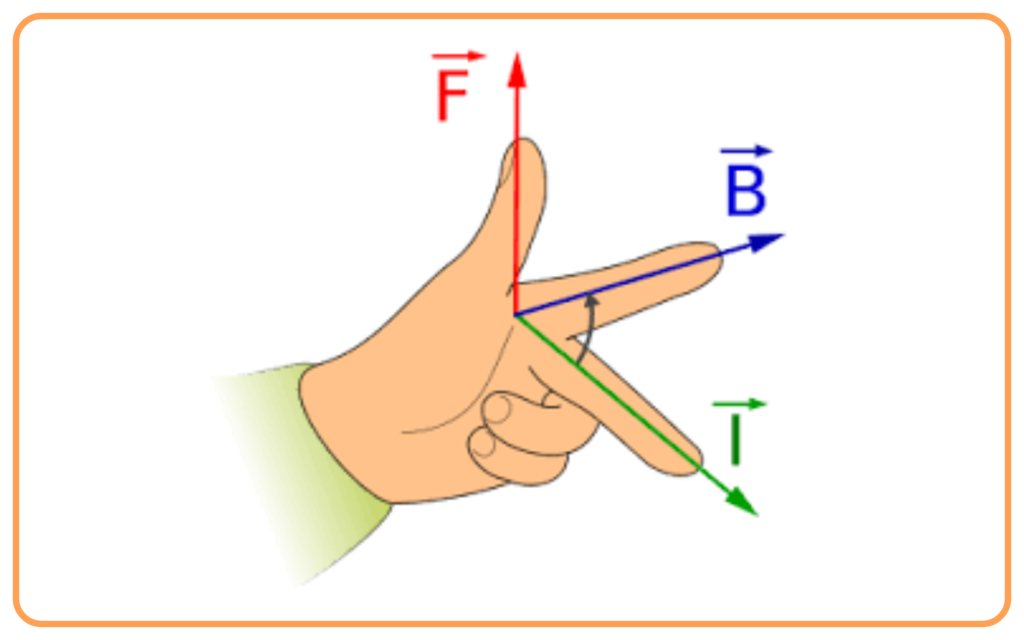
• Stretch the thumb, forefinger, and middle finger of your left hand at right angles to each other:
  • Forefinger → Direction of the magnetic field (B).
  • Middle finger → Direction of the current (I).
  • Thumb → Direction of the force (F).

Real-Life Applications

• Electric Motors: This principle is used to generate rotational motion in electric motors.

• Loudspeakers: The force causes vibrations in a diaphragm, producing sound.

• Moving Coil Galvanometer: Used to measure small electric currents.

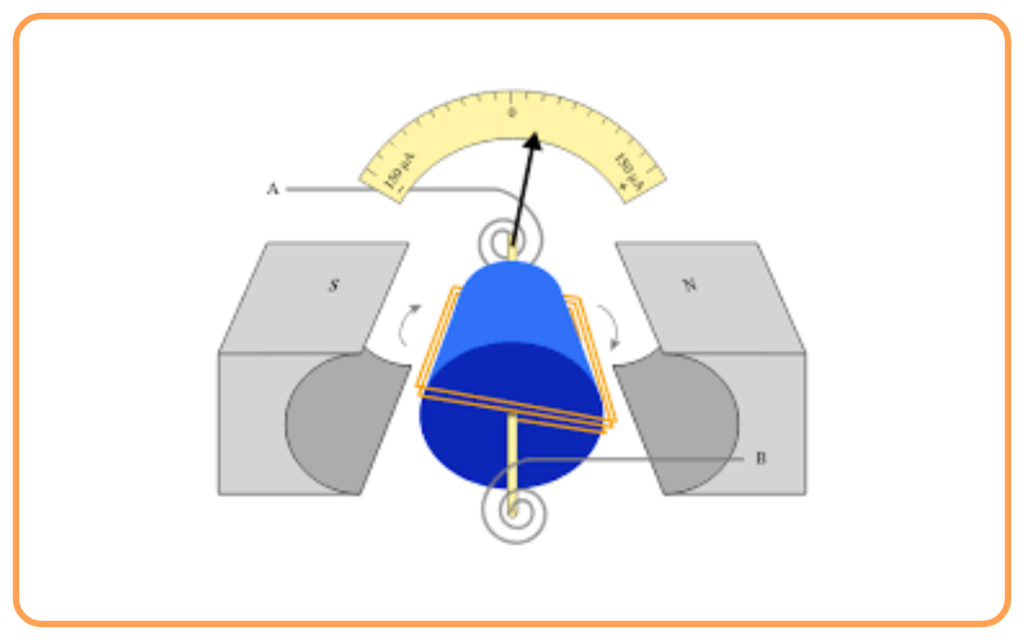
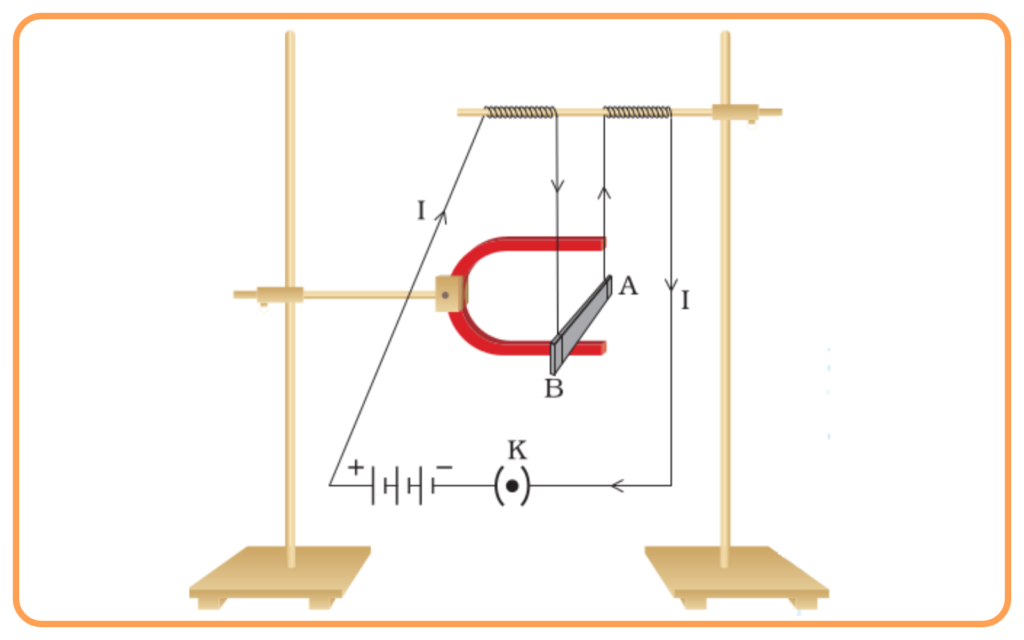
Demonstration Experiment

• Place a current-carrying conductor in a magnetic field between two magnets (north and south poles).
• Observe the movement of the conductor when current flows.
• Change the direction of the current or the magnetic field:
  • The conductor’s direction of motion reverses.