Trigonometric ratios: sin, cos and tan
Key notes :
1. Introduction to Trigonometric Ratios
- Trigonometric ratios are used to relate the angles of a right triangle to the lengths of its sides.
- These ratios are fundamental for solving problems involving right-angled triangles and are widely used in geometry, physics, engineering, and various other fields.
2. Basic Trigonometric Ratios
In a right-angled triangle, for an angle θ\thetaθ, the three primary trigonometric ratios are:
Sine (sin)
- The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse.

Cosine (cos)
- The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse.
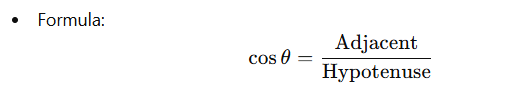
3. Relationship Between the Trigonometric Ratios
- The three basic trigonometric ratios are interrelated. For example:

4. Reciprocal Trigonometric Ratios
- Cosecant (csc): The reciprocal of sine:

Secant (sec): The reciprocal of cosine:

Cotangent (cot): The reciprocal of tangent:
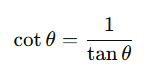
Learn with an example
Find the sine of ∠Y.

Simplify your answer and write it as a proper fraction, improper fraction, or whole number.
sin(Y)= ______
Take the formula for the sine of ∠Y and plug in the relevant side lengths.

sin ( Y ) = opp / hyp Definition of sine
= WX / XY Substitute opp=WX and hyp=XY
= 56 / 65 Plug in WX=56 and XY=65
So, sin(Y)= 56/65 ,
Find the cosine of ∠T.

Simplify your answer and write it as a proper fraction, improper fraction, or whole number.
cos(T)= ______
Take the formula for the cosine of ∠T and plug in the relevant side lengths.
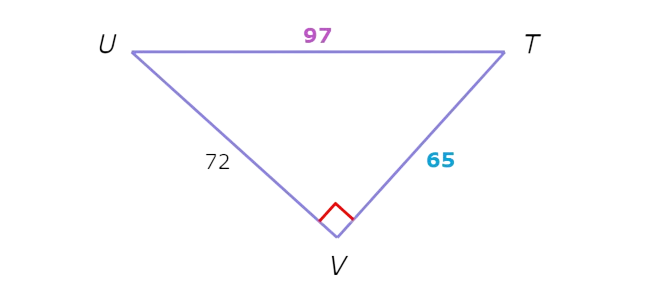
cos ( T ) = adj / hyb Definition of cosine
= TV / TU Substitute adj=TV and hyp=TU
= 65 / 97 Plug in TV=65 and TU=97
So, cos(T) = 65/97 .
Find the cosine of ∠U.

Simplify your answer and write it as a proper fraction, improper fraction, or whole number.
cos(U)= _______
Take the formula for the cosine of ∠U and plug in the relevant side lengths.

cos ( U ) = adj / hyb Definition of cosine
= UV / TU Substitute adj= UV and hyp= TU
= 5/13 Plug in UV=5 and TU=13
So, cos(U)= 5/13 .
let’s practice!

