Inscribed angles
key notes :
1. Definition of Inscribed Angle:
- An inscribed angle is an angle formed by two chords in a circle that have a common endpoint. This common endpoint is the vertex of the angle, and the sides of the angle are the chords of the circle.
2. Relationship with the Arc:
- The inscribed angle intercepts a part of the circle’s circumference called the arc.
- The measure of an inscribed angle is half the measure of the intercepted arc.
Formula:
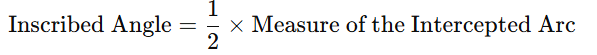
Example: If the intercepted arc is 60°, the inscribed angle will be 30°.
3. Inscribed Angles Subtended by the Same Arc:
- Angles subtended by the same arc on the circle are equal.
- This means that any two inscribed angles that intercept the same arc will have the same measure.
4. Inscribed Angle in a Semicircle:
- An inscribed angle that subtends a diameter of the circle is always a right angle (90°).
- This is known as Thales’ Theorem.
5. Cyclic Quadrilaterals:
- A cyclic quadrilateral is a quadrilateral whose vertices lie on the circumference of a circle.
- The opposite angles of a cyclic quadrilateral are supplementary (i.e., their sum is 180°).
6. Application of Inscribed Angles:
- To find the angle between two chords.
- To calculate unknown angles in cyclic quadrilaterals.
- To solve problems involving tangents and secants.
7. Important Theorems:
- Angle at the Center vs. Angle at the Circumference:
- The angle at the center of a circle is twice the angle at the circumference subtended by the same arc.
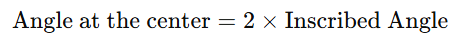
- Angle between a Chord and a Tangent:
- The angle between a tangent and a chord through the point of contact is equal to the inscribed angle subtended by the chord on the opposite side of the tangent.
8. Examples:
- If an inscribed angle intercepts an arc of 120°, the angle will measure 60°.
- In a circle with a diameter as a chord, the inscribed angle will always be a right angle (90°).
Learn with an example
What is ∠HGI?
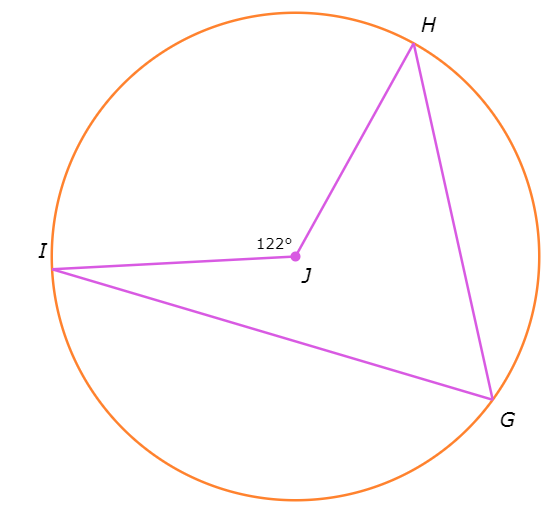
∠HGI= _____∘
Look at the diagram:
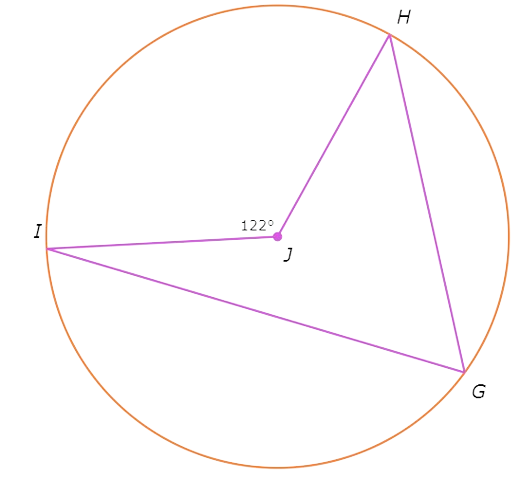
∠HGI is an inscribed angle that intercepts the same arc as the central angle ∠J, so use the Inscribed Angle Theorem.
∠HGI =1/2 . ∠j
=1/2 (122°) plug ∠J=122°
=61°
∠HGI is 61°.
What is ∠F?
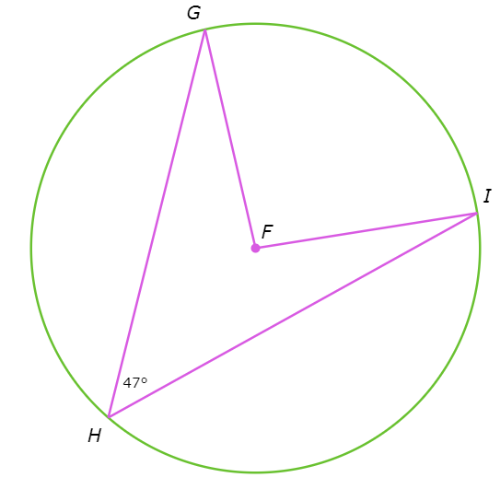
∠F= ________°
Look at the diagram:
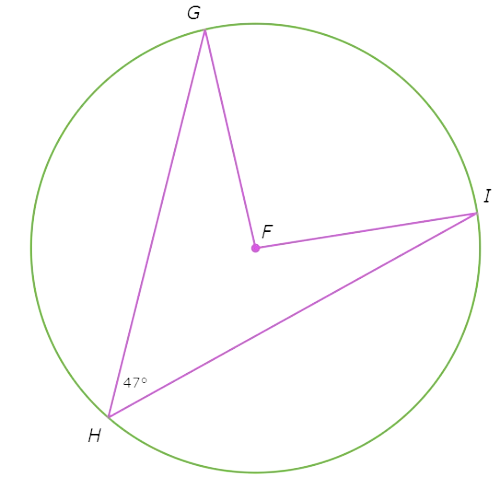
∠GHI is an inscribed angle that intercepts the same arc as the central angle ∠F, so use the Inscribed Angle Theorem.
∠F= 2 . ∠GHI Inscribed Angle Theorem
= 2 .(47°) Plug in ∠GHI=47°
= 94° Multiply
∠F is 94°.
What is ∠J?
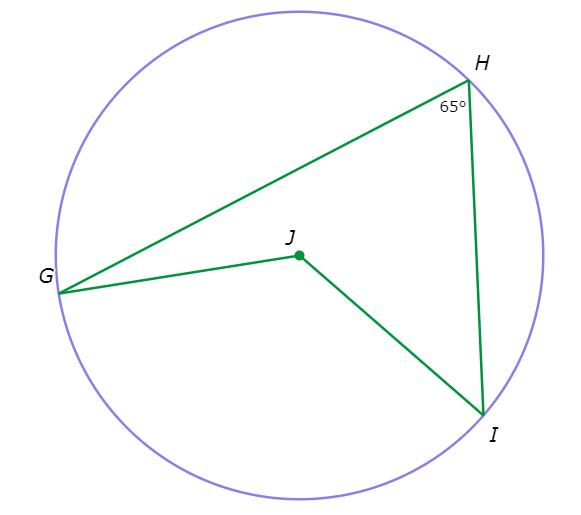
∠J=______ °
Look at the diagram:
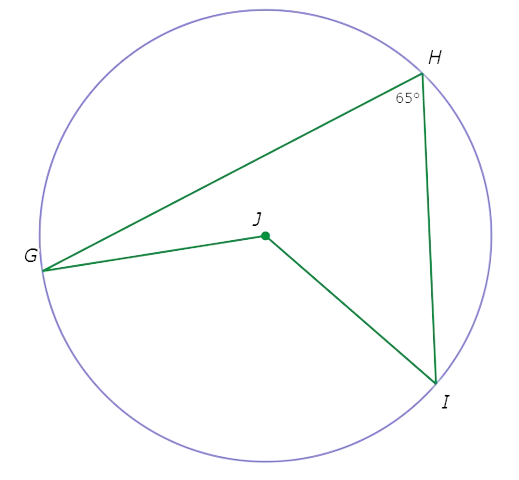
∠GHI is an inscribed angle that intercepts the same arc as the central angle ∠J, so use the Inscribed Angle Theorem.
∠J = 2 . ∠GHI Inscribed Angle Theorem
= 2 . (65°) Plug in ∠GHI=65°
= 130° Multiply
∠J is 130°.
let’s practice!

