Arcs and chords
Key Notes :
Arclength is the distance between two points along a section of a curve or circle.
Here is a formula for arc length:
𝓁= m/360 . C
In the formula, 𝓁 is the arc length, m is the degree measure of an arc (or the central angle that intercepts the arc), and C is the circumference of the circle.
🔔 Tip
You can also write this formula as a proportion where each ratio relates the arc to the full circle:
𝓁/C = m/360
The ratio 𝓁/C compares the arc length to the circumference of the circle. The ratio m/360 compares the degree measure of the arc to the degree measure of a full circle.
Finding arc length
Let’s try it! The radius of the circle below is 8 feet. Find the length of a 120° arc.
To find the arc’s length, you’ll need to use the arc’s measure and the circle’s circumference. Find the circle’s circumference using the formula C=2𝜋r, where r is the radius.
C=2𝜋r
= 2 . 𝜋 . 8 Plug in r=8.
= 16𝜋 Simplify.
The circumference is 16𝜋 feet.
Now, find the length of the arc.
𝓁= m / 360 . C
= 120 / 360 . 16𝜋 Plug in m=120 and C=16𝜋.
= 16𝜋 / 3 Simplify.
So, the length of the arc is 16𝜋 / 3 feet
Finding arc measures
To find the measure of an arc, you can use the arc’s length and the circle’s circumference.
Let’s try it! The diameter of the circle below is 12 inches. Find the measure, in degrees, of an arc that is 2𝜋 inches long.
To find the arc’s measure in degrees, you’ll need to use the arc’s length and the circle’s circumference. Find the circle’s circumference using the formula C=𝜋d, where d is diameter.
C=𝜋d
= 12𝜋 Plug in d=12.
The circumference is 12𝜋 inches.
Now, find the measure of the arc.
𝓁= m / 360 . C
2𝜋= m / 360 . 12𝜋 Plug in 𝓁=2𝜋 and C=12𝜋
2𝜋 . 360 / 12𝜋 = m Multiply both sides by 360 / 12𝜋
60= m Simplify
So, the measure of the arc is 60°.
Arc length and radians
You can also find arc length when the arc or the central angle is measured in radians. Here is a formula for arc length:
𝓁=r𝜃
In the formula, 𝓁 is the arc length, r is the radius of the circle, and 𝜃 is the radian measure of the arc (or the central angle that intercepts the arc).
🔔 Tip
When using this formula to solve problems, you may be asked about an arc that subtends a given angle. This means that the endpoints of the arc are the points where the angle intersects the circle.
For example, in the circle below, BC subtends ∠BAC
Finding arc length
Let’s try it! The radius of the circle below is 12 centimeters. Find the length of an arc that subtends an angle of 𝜋/2 radians.
You can use the central angle’s measure and the circle’s radius to find the arc’s length.
𝓁=r𝜃
=12 . 𝜋/2 Plug in r=12 and 𝜃= 𝜋/2
= 6𝜋 Simplify.
So, the length of the arc is 6𝜋 centimeters.
Finding arc measures
You can use an arc’s length and the circle’s radius to find an arc’s measure in radians.
Let’s try it! The radius of the circle below is 3 meters. Find the measure, in radians, of an arc that is 5𝜋/2 meters long.
Find the measure of the arc using the arc’s length and the circle’s radius.
𝓁=r𝜃
5𝜋/2 = 3𝜃 Plug in 𝓁= 5𝜋/2 and r = 3
5𝜋/6 = 𝜃 Divide both sides by 3.
So, the measure of the arc is 5𝜋/6 radians
🔔 Fun Fact
The formula 𝓁=r𝜃 comes from the definition of radians. The radian measure of a central angle in a circle is 𝜃=𝓁/r, where 𝓁 is the length of the arc that the angle intercepts, and r is the radius of the circle. You can solve that equation for 𝓁 to get the formula.
𝜃=𝓁/r Definition of radian
r𝜃= 𝓁 Multiply both sides by r.
Learn with an example
What is the length of ST ?
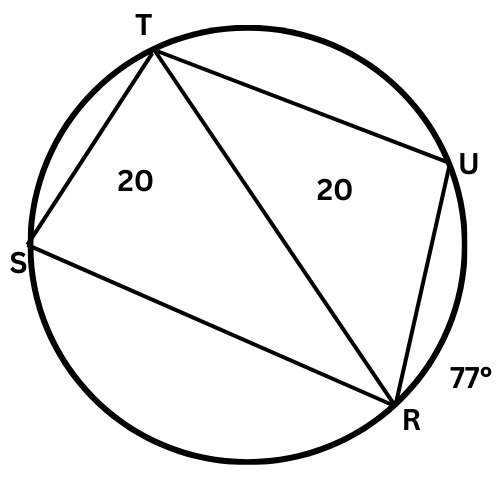
ST = _______°
RU and ST are arcs in a circle, and their corresponding chords are congruent. So, RU is congruent to ST.
ST=RU=77°.
What is the measure of CD ?
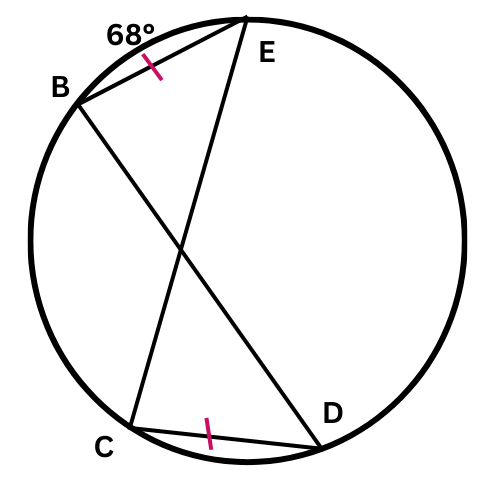
CD = ________°
BE and CD are arcs in a circle, and their corresponding chords are congruent. So, BE is congruent to CD.
CD = BE = 68°.
What is the measure of HI ?
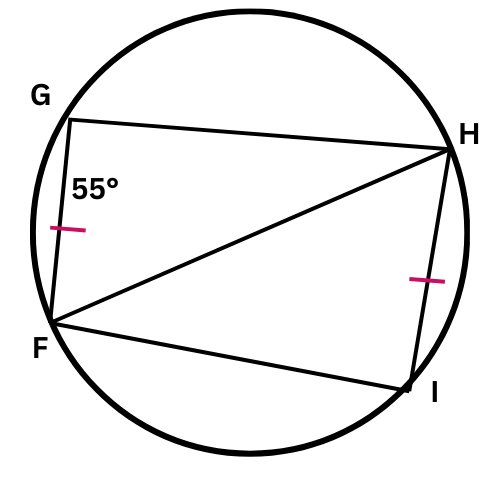
HI = _______°
FG and HI are arcs in a circle, and their corresponding chords are congruent. So, FG is congruent to HI.
HI=FG=55°.
let’s practice!

