Angles in inscribed quadrilaterals
Key Notes :
1. Definition
An inscribed quadrilateral is a four-sided polygon whose vertices all lie on the circumference of a circle. It is also called a cyclic quadrilateral.
2. Properties of Inscribed Quadrilaterals
Opposite Angles are Supplementary:
The sum of the measures of opposite angles in an inscribed quadrilateral is always 1800.
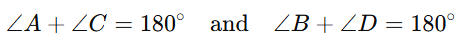
- Exterior Angle Property:The exterior angle of an inscribed quadrilateral is equal to the interior opposite angle.
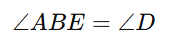
3. Cyclic Quadrilateral Conditions
A quadrilateral can be inscribed in a circle if:
- The opposite angles are supplementary.
- The perpendicular bisectors of the sides of the quadrilateral meet at the center of the circumscribing circle.
4. Theorems Related to Inscribed Quadrilaterals
- Angle Sum Theorem:
The sum of all angles in any quadrilateral is 3600 .
For an inscribed quadrilateral:
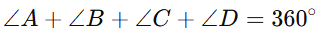
- Converse of the Opposite Angle Theorem:If the sum of opposite angles of a quadrilateral is 1800, then the quadrilateral can be inscribed in a circle.
Learn with an example
➡️ What is ∠D?
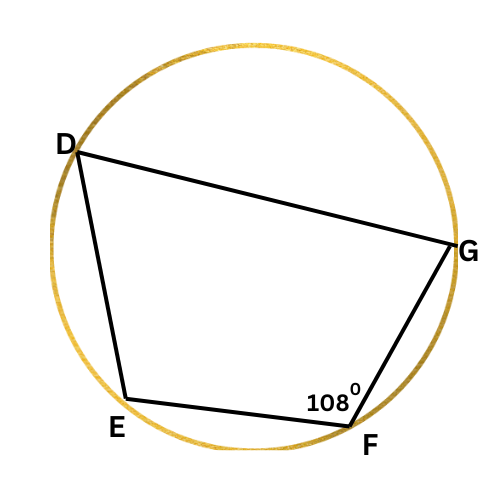
∠D=_____ °
Look at the diagram:
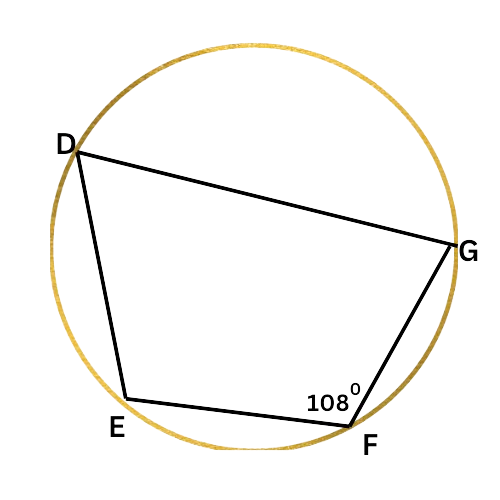
Since DEFG is an inscribed quadrilateral, ∠F and ∠D are supplementary. Write an equation setting the sum of their measures equal to 180°, and solve for ∠D.
∠F+∠D=180°
108°+∠D=180° Plug in ∠F=108°
∠D=72° Subtract 108° from both sides
∠D is 72°.
➡️ What is ∠H?
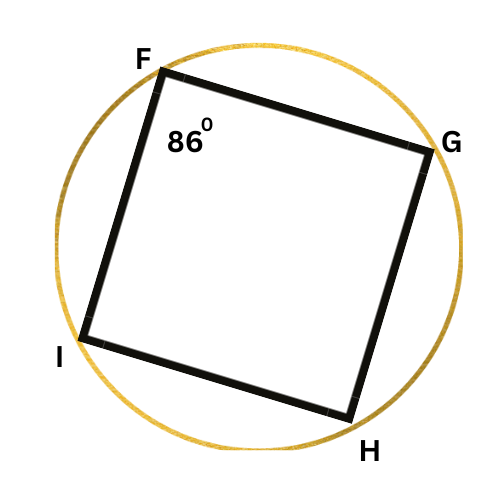
∠H=______ °
Look at the diagram:
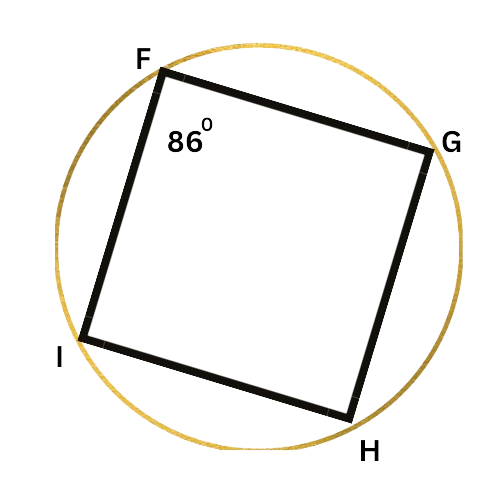
Since FGHI is an inscribed quadrilateral, ∠F and ∠H are supplementary. Write an equation setting the sum of their measures equal to 180°, and solve for ∠H.
∠F+∠H=180°
86°+∠H=180° Plug in ∠F=86°
∠H=94° Subtract 86° from both sides
∠H is 94°.
➡️ What is ∠G?
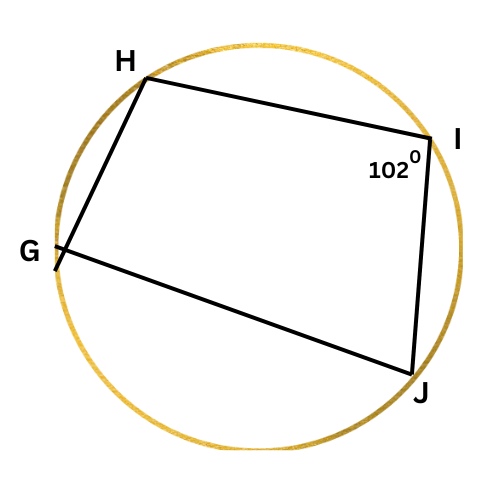
∠G=________ °
Look at the diagram:
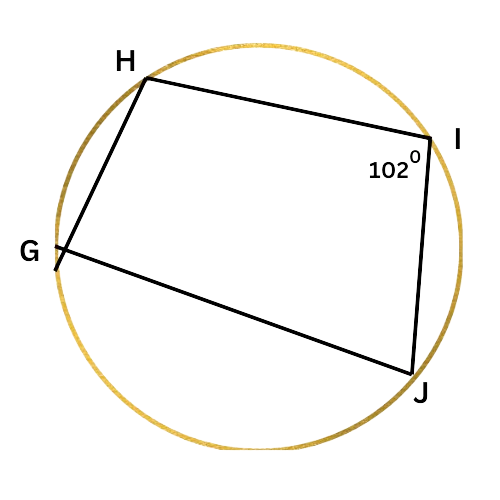
Since GHIJ is an inscribed quadrilateral, ∠I and ∠G are supplementary. Write an equation setting the sum of their measures equal to 180°, and solve for ∠G.
∠I+∠G=180°
102°+∠G=180° Plug in ∠I=102°
∠G=78° Subtract 102° from both sides
∠G is 78°.
let’s practice!

