Pythagoras’ Inequality Theorems
Key Notes :
If a, b, and c are the side lengths of a triangle and a≤b≤c, then:
a2+b2>c2 if and only if the triangle is acute.
a2+b2=c2 if and only if the triangle is right.
a2+b2<c2 if and only if the triangle is obtuse.
Learn with an example
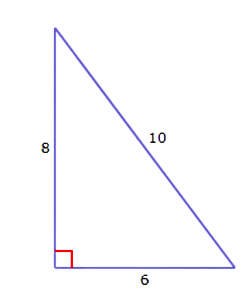
📚 The sides of a triangle have lengths 6, 8, and 10. What kind of triangle is it?
- acute
- right
- obtuse
- First, put the three side lengths in order from smallest to largest: a=6, b=8, c=10.
- To classify the triangle, compare a2+b2 to c2.
- a2+b2 ? c2
- 62+82 ? 102
- 36+64 ? 100
- 100 = 100
- Since 62+82=102, these are the side lengths of a right triangle:
📚 The sides of a triangle have lengths 3, 4, and 5. What kind of triangle is it?
- acute
- right
- obtuse
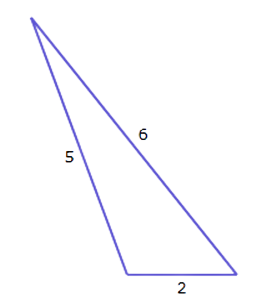
- First, put the three side lengths in order from smallest to largest: a=2, b=5, c=6.
- To classify the triangle, compare a2+b2 to c2.
- a2+b2 ? c2
- 22+52 ? 62
- 4+25 ? 36
- 29 < 36
- Since 22+52<62, these are the side lengths of an obtuse triangle:
📚 The sides of a triangle have lengths 5, 9, and 9. What kind of triangle is it?
acute
right
obtuse
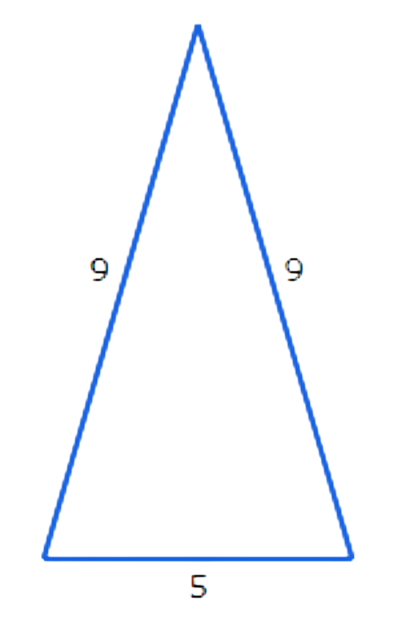
First, put the three side lengths in order from smallest to largest: a=5, b=9, c=9.
To classify the triangle, compare a2+b2 to c2.
a2+b2 ? c2
52+92 ? 92
25+81 ? 81
106 > 81
Since 52+92>92, these are the side lengths of an acute triangle:
Let’s practice!

