Pythagoras’ Theorem
Key Notes :
📚 In a right triangle, a2 + b2 = c2, where a and b are the lengths of the legs and c is the length of the hypotenuse. This is called Pythagoras’ theorem.
Learn with an example
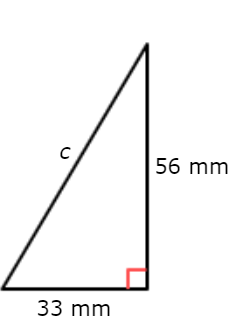
What is the perimeter?
________ millimetres
Use Pythagoras’ theorem, with a = 56 and b = 33.
a2 + b2= c2 Pythagoras’ theorem
562 + 332= c2 Plug in a = 56 and b = 33
3,136 + 1,089 = c2 Square
4,225 = c2 Add
√4225 = √c2 Take the square root of both sides
65 = c Simplify
The length of the hypotenuse is 65 millimetres.
Find the perimeter. Add the lengths of the two sides and the hypotenuse.
a + b +c = 56 + 33 +65
= 154
The perimeter is 154 millimetres.
Marco’s school is due west of his house and due south of his friend Jonah’s house. The distance between the school and Jonah’s house is 15 kilometres and the straight-line distance between Marco’s house and Jonah’s house is 17 kilometres. How far is Marco’s house from school?
_______ Kilometres
Draw a diagram.

Use Pythagoras’ theorem, with a = 15 and c = 17.
a2 + b2= c2 Pythagoras’ theorem
152 + b2= 172 Plug in a = 15 and c = 17
225+ b2 = 289 Square
b2 = 64 Add
√b2 = √64 Take the square root of both sides
b = 8 Simplify
Marco’s house is 8 kilometres from school.
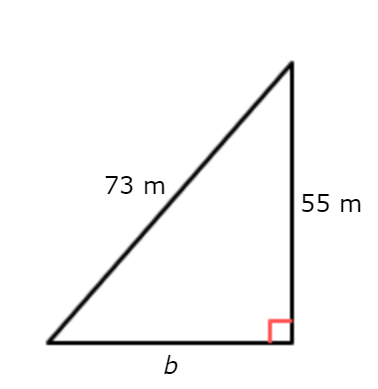
What is the length of the missing leg?
b = _______ metres
Use Pythagoras’ theorem, with a = 55 and c = 73.
a2 + b2= c2 Pythagoras’ theorem
552 + b2= 732 Plug in a = 15 and c = 17
3025+ b2 = 5329 Square
b2 = 2304 Add
√b2 = √2304 Take the square root of both sides
b = 48 Simplify
The length of the missing leg is 48 metres.
Let’s practice!

