Areas of similar figures
Key Notes :
The following proportion applies to similar shapes:
(a / b )2 = A1 / A2
where a / b is the ratio of the corresponding side lengths, and A1 / A2 is the ratio of the areas.
Learn with an example
The figures below are similar. The labelled sides are corresponding.
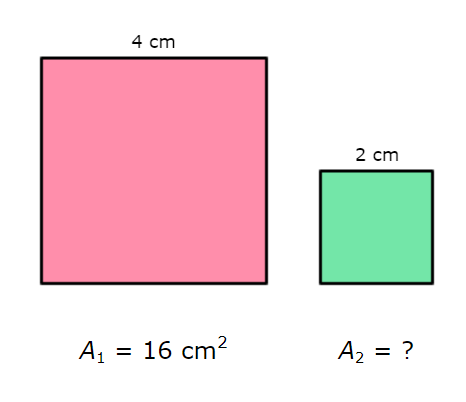
What is the area of the smaller square?
A2 = _______ square centimetres
Find the square of the ratio of the corresponding side lengths.
(a / b )2 = (4 / 2)2 = (2 / 1)2 = 4/1
Find the ratio of the areas.
A1 / A2 = 16 / A2
Use these two ratios to set up a proportion and solve for A2.
4 / 1 = 16 / A2
4 / 1 (A2) = 16 / A2 (A2) Multiply both sides by A2
4 A2 = 16 .1 Simplify
4 A2 = 16 Simplify
4 A2 ÷ 4 = 16 ÷ 4 Divide both sides by 4
A2 = 4
The area of the smaller square is 4 square centimetres.
The figures below are similar. The labelled sides are corresponding.
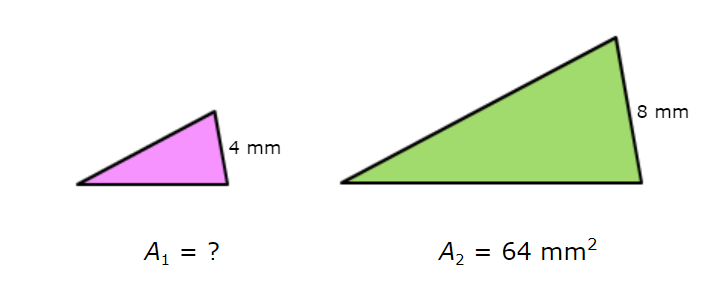
What is the area of the smaller triangle?
A1 = _______ square centimetres
Find the square of the ratio of the corresponding side lengths.
(a / b )2 = (4 / 8)2 = (1 / 2)2 = 1 / 4
Find the ratio of the areas.
A1 / A2 = A1 / 64
Use these two ratios to set up a proportion and solve for A1.
1 / 4 = A1 / 64
1 / 4 (4 . 64 ) = A1 / 64 (4 . 64 ) Multiply both sides by 4 · 64
1 . 64 = 4A1 Simplify
64 = 4A1 Simplify
64 ÷ 4 = 4A1 ÷ 4 Divide both sides by 4
16 = A1
The area of the smaller triangle is 16 square millimetres.
The figures below are similar. The labelled sides are corresponding.

What is the area of the smaller rectangle?
A1 = _______ square centimetres
Find the square of the ratio of the corresponding side lengths.
(a / b )2 = (2 / 5)2 = (4 / 25)
Find the ratio of the areas.
A1 / A2 = A1 / 100
Use these two ratios to set up a proportion and solve for A1 .
4 / 25 = A1 / 100
4 / 25 (25 . 100 ) = A1 / 100 (25 . 100 ) Multiply both sides by 25 . 100
4 . 100 = 25A1 Simplify
400 = 25A1 Simplify
400 ÷ 25 = 25A1 ÷ 25 Divide both sides by 25
16 = A1
The area of the smaller rectangle is 16 square millimetres.
Let’s practice!

