You can transform △GHI to △G‘H‘I‘ by translating it and then performing a dilation centered at the origin. So, △GHI~△G‘H‘I‘. Find the translation rule and the scale factor of the dilation.

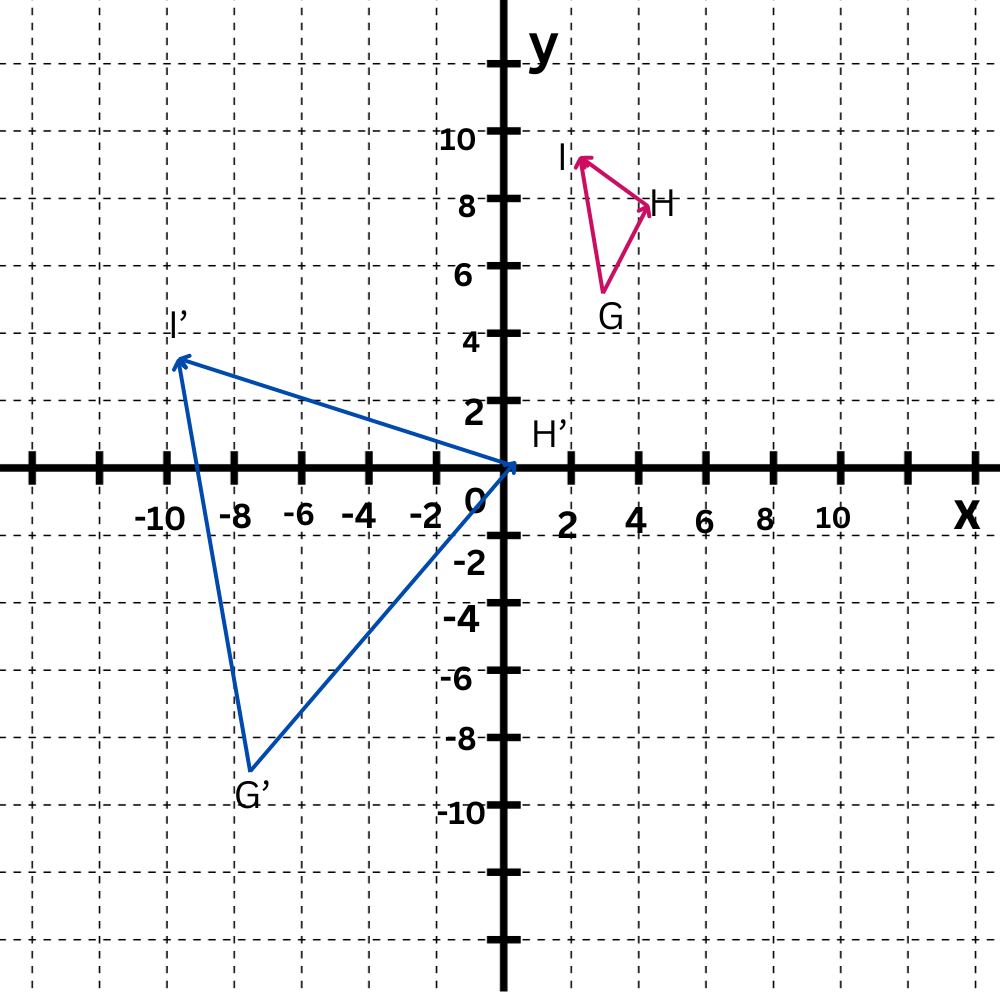
Simplify the scale factor and write it as a proper fraction, improper fraction, or whole number.

Translation : (X , Y) ↦ ( _____,_____ )

Scale factor: _______

△G‘H‘I‘ is a translation and dilation of △GHI, so △GHI~△G‘H‘I‘. This means that G corresponds to G‘,H to H‘, and I to I‘.

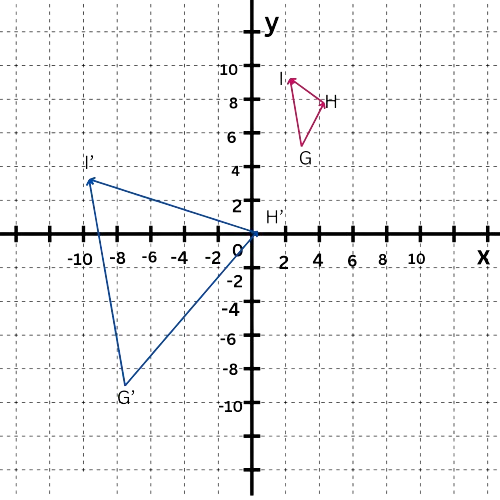
Since the dilation is centred at the origin, make sure that one pair of corresponding vertices is located at the origin before you apply the dilation. This makes sure that the dilation will not affect the coordinates of these points. (In general, it is always the case that the centre of the dilation is not affected by the dilation.)

From the diagram, you can see that H‘ is already located at the origin. So, find the translation that maps H(4,8) to H‘(0,0).

To translate H(4, 8) to H‘(0, 0), move 4 units to the left and 8 units down. So, the translation that maps H to H‘ is given by the rule (x , y)↦(x–4,y–8). Next, apply this translation rule to the three vertices of △GHI. The image of H is H‘, the image of GH lies on top of G‘H‘ , and the image of HI lies on top of H‘I‘.

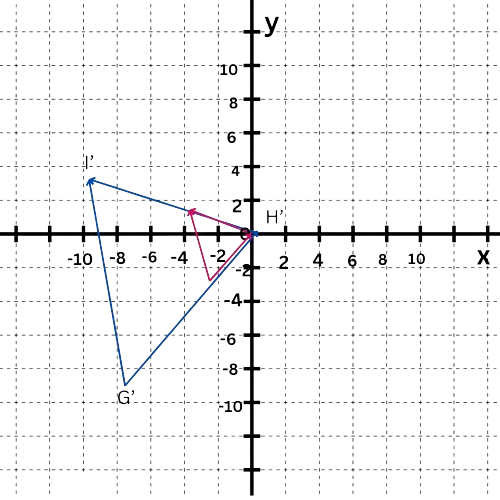
Now, find the scale factor of the dilation that will expand the image of △GHI onto △G‘H‘I‘. Choose a pair of corresponding vertices not located at the origin, like I‘(–9,3) and the image of I after the translation, which is (–3,1).

Calculate the ratio of the x-coordinates or the ratio of the y-coordinates. For instance, the ratio of the y-coordinates is 3 / 1=3, so the scale factor of the dilation that maps (–3,1) onto I‘(–9,3) is 3. This dilation also maps the image of G, which is (–2,–3), onto G‘(–6,–9), and fixes both H and H‘.

In summary, the translation and scale factor are:

Translation: (X , Y) ↦ (X-4 , Y-8)

Scale factor: 3

You can transform △UVW to △U‘V‘W‘ by translating it and then performing a dilation centered at the origin. So, △UVW~△U‘V‘W‘. Find the translation rule and the scale factor of the dilation.

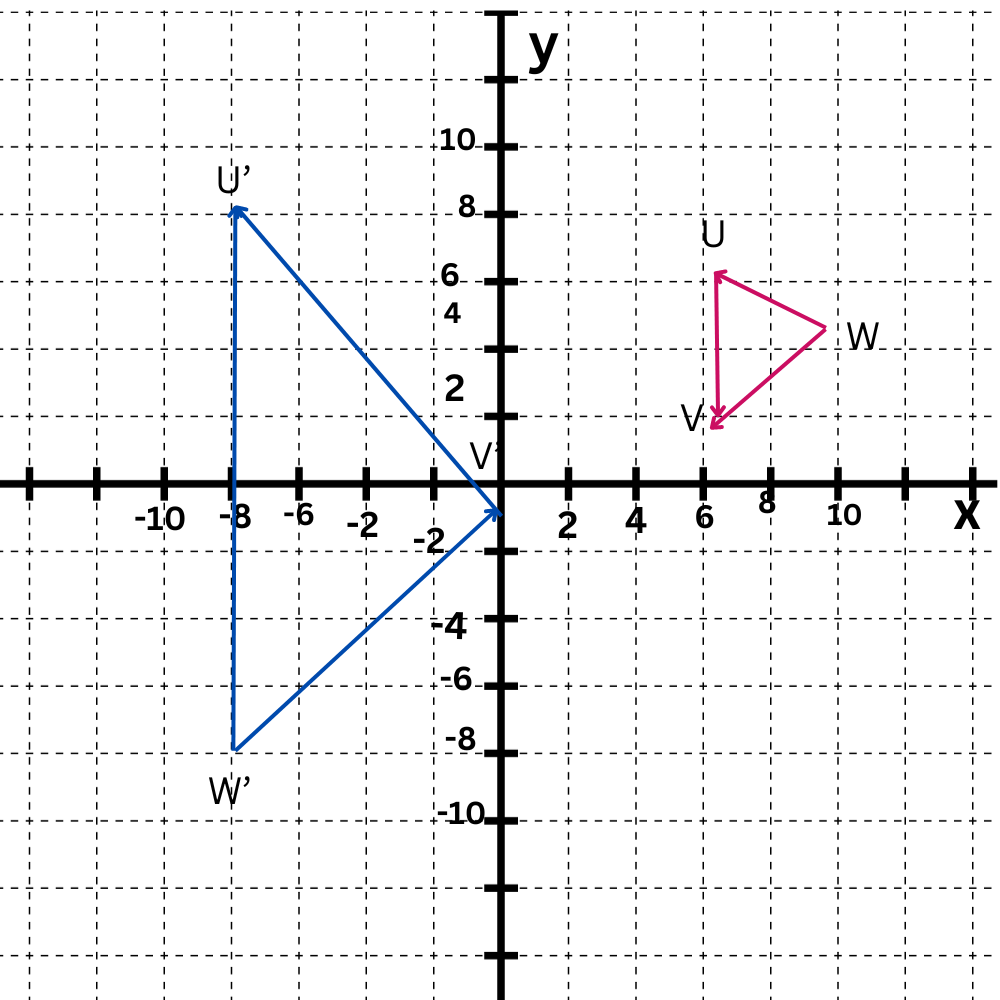
Simplify the scale factor and write it as a proper fraction, improper fraction, or whole number.

Translation : (X , Y) ↦ ( _____,_____ )

Scale factor: _______

△U‘V‘W‘ is a translation and dilation of △UVW, so △UVW~△U‘V‘W‘. This means that U corresponds to U‘, V to V‘, and W to W‘.

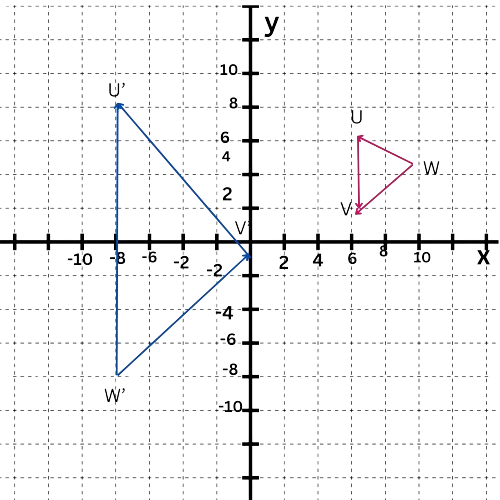
Since the dilation is centred at the origin, make sure that one pair of corresponding vertices is located at the origin before you apply the dilation. This makes sure that the dilation will not affect the coordinates of these points. (In general, it is always the case that the centre of the dilation is not affected by the dilation.)

From the diagram, you can see that V‘ is already located at the origin. So, find the translation that maps V(9, 4) to V‘(0,0).

To translate E(9, 4) to V‘(0,0), move 9 units to the left and 4 unit down. So, the translation that maps V to V’ is given by the rule (x , y)↦(x–9,y-4). Next, apply this translation rule to the three vertices of △UVW. The image of V is V‘, the image of UV lies on top of U‘V‘ , and the image of VW lies on top of V‘W‘.

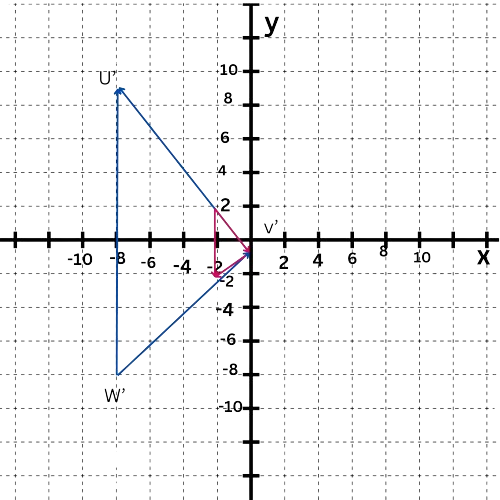
Now, find the scale factor of the dilation that will expand the image of △UVW onto △U‘V‘W‘. Choose a pair of corresponding vertices not located at the origin, like U‘(–8,8) and the image of U after the translation, which is (–2,2).

Calculate the ratio of the x-coordinates or the ratio of the y-coordinates. For instance, the ratio of the y-coordinates is 8 / 2=4, so the scale factor of the dilation that maps (–2,2) onto U‘(–8,8) is 4. This dilation also maps the image of W, which is (–2,–2), onto W‘(–8,–8), and fixes both V and V‘.

In summary, the translation and scale factor are:

Translation: (X , Y) ↦ (X-9 , Y-4)

Scale factor: 4