Are these triangles similar?

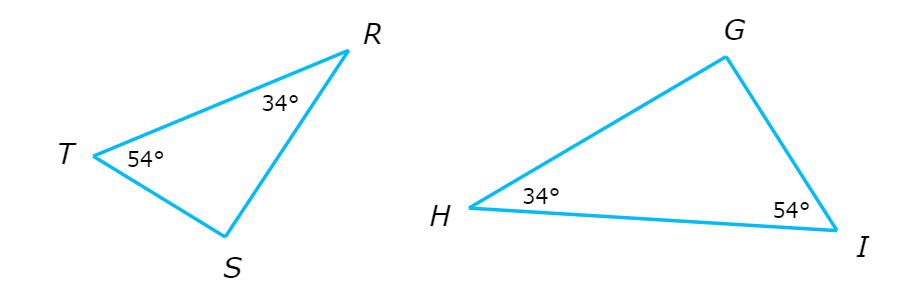
• Yes
• No

Look at the diagram.

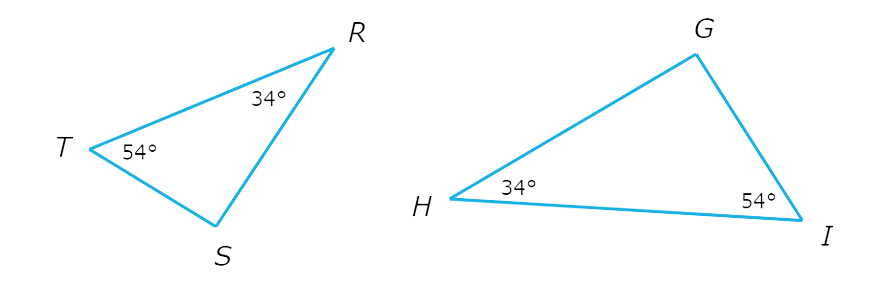
Since ∠T=∠I=54°and ∠R=∠H=34°,∠T ≅ ∠I and  ∠R ≅ ∠H.

Therefore, by the AA Similarity Theorem the triangles are similar.

To write the similarity statement, match corresponding vertices: 

△RST ~ △HGI.

Are these triangles similar?

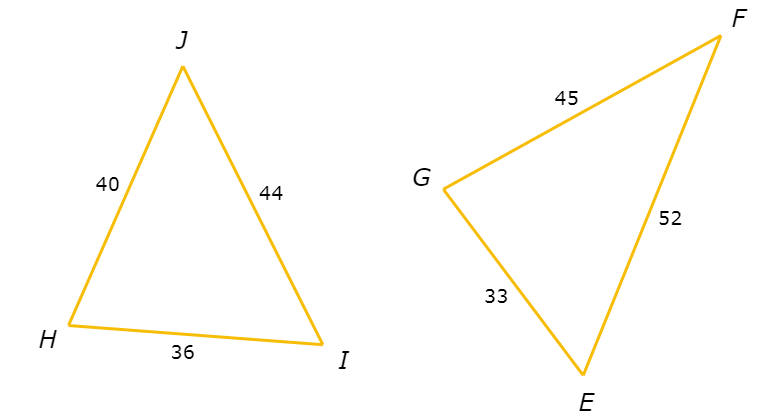
• Yes
• No

Since all three side lengths of △HIJ and △EFG are given, see if these triangles are similar by the SSS Similarity Theorem.

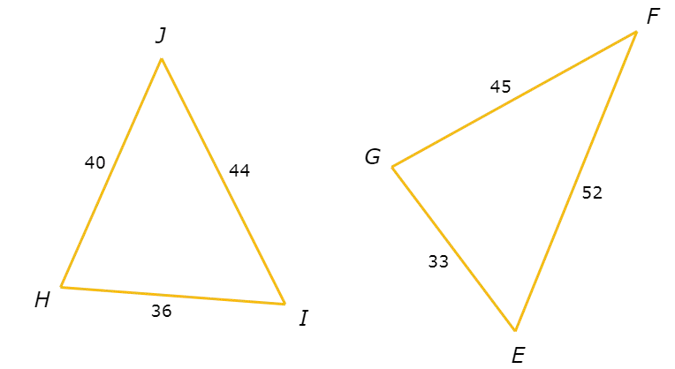
Remember that two triangles are similar if and only if they are scaled versions of each other. So, the shortest, middle, and longest sides in similar triangles are always corresponding. Therefore, if the ratios of the shortest, middle, and longest side lengths are not equal, the triangles are not similar.

Pair the sides in order from shortest to longest:  HI and EG , HJ and FG, and IJ and  EF .

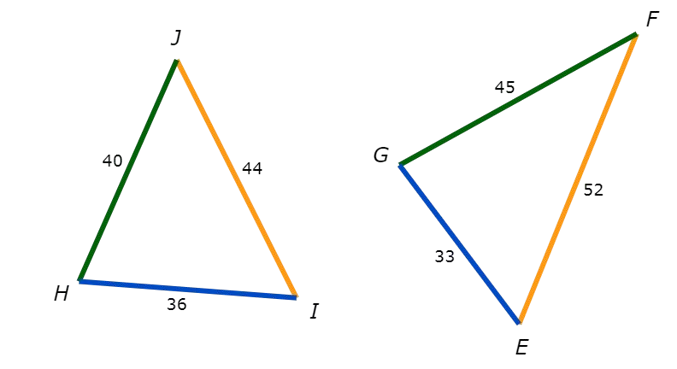
Calculate the ratios of these three pairs of side lengths.

HI / EG = 36 / 33 = 12 / 11

HJ / FG = 40 / 45 = 8 / 9

IJ / EF = 44 / 52 = 11 / 13

Since HI / EG ≠ HJ / FG , not all three pairs of sides are proportional. Therefore, the triangles are not similar.

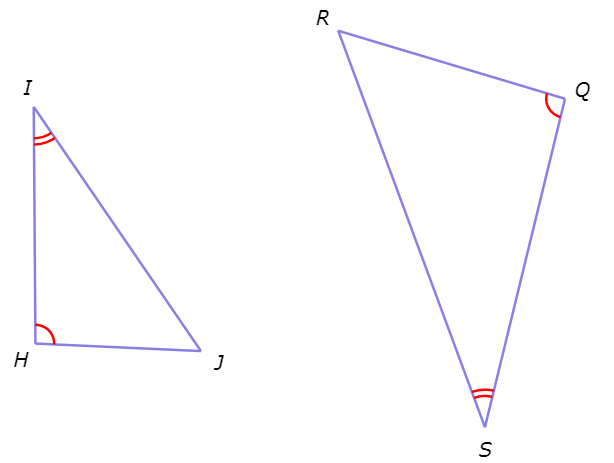
Are these triangles similar?

• Yes
• No

Look at the diagram.

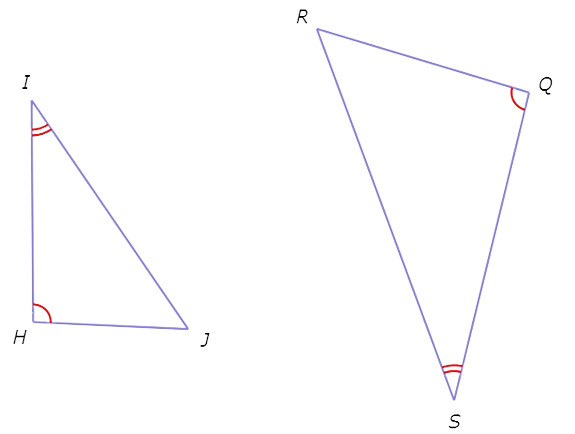
∠H ≅ ∠Q and ∠I ≅ ∠S.

Therefore, by the AA Similarity Theorem the triangles are similar.

To write the similarity statement, match corresponding vertices: 

△HIJ ~ △QSR.