Similar triangles and indirect measurement
Key Notes :
The sides of similar triangles are proportional.
Learn with an example
Find r.
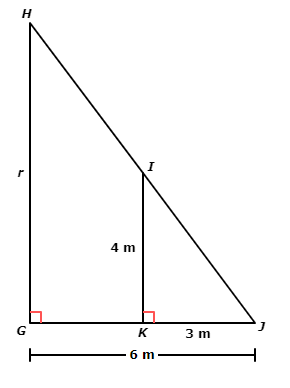
Write your answer as a whole number or a decimal. Do not round.
r = _______ metres
The original diagram included a smaller triangle inside a larger triangle. Redraw them as separate triangles.

△KJI is similar to △GJH because all three pairs of corresponding angles are congruent.
One pair of corresponding side lengths is KJ and GJ .Together they form the fraction KJ / GJ
An other pair of corresponding side lengths is IK and HG. Together they form the fraction IK / HG .
In both fractions, the numerator comes from △KJI and the denominator comes from △GJH Since the triangles are similar, you can use the fractions to set up a proportion and solve for r.
KJ / GJ = IK / HG
3 / 6 = 4 / r Plug in the side lengths
3 / 6 (6r) = 4 / r (6r) Multiply both sides by 6r
3 r = 4 . 6 Simplify
3r = 24 Simplify
3r ÷ 3 = 24 ÷ 3 Divide both sides by 3
r = 8
The missing length is 8 metres.
In the diagram below, △GHD ~ △ EFD . Find w.
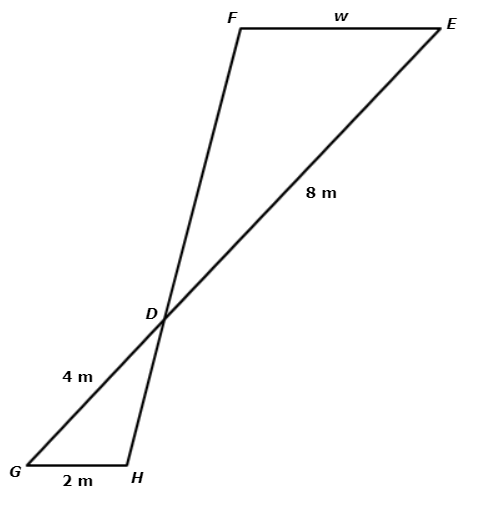
Write your answer as a whole number or a decimal. Do not round.
w = _______ metres
The original diagram included a smaller triangle and a larger triangle. Redraw them as separate triangles with corresponding sides in the same colour.
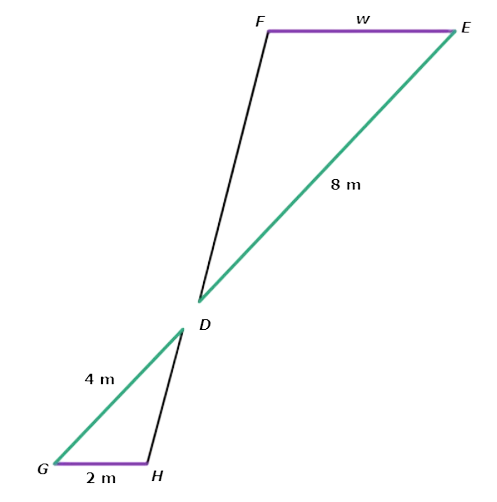
△GHD ~ △ EFD means that △GHD is similar to △ EFD
One pair of corresponding side lengths is DG and DE. Together they form the fraction DG / DE .
Another pair of corresponding side lengths is GH and EF. Together they form the fraction GH / EF .
In both fractions, the numerator comes from △GHD and the denominator comes from △ EFD .Since the triangles are similar, you can use the fractions to set up a proportion and solve for w.
DG / DE = GH / EF
4 / 8 = 2 / w Plug in the side lengths
4 / 8 (8w) = 2 / w (8w) Multiply both sides by 8w
4 w = 2 . 8 Simplify
4w = 16 Simplify
4w ÷ 4 = 16 ÷ 4 Divide both sides by 4
w = 4
The missing length is 4 metres.
Find k.
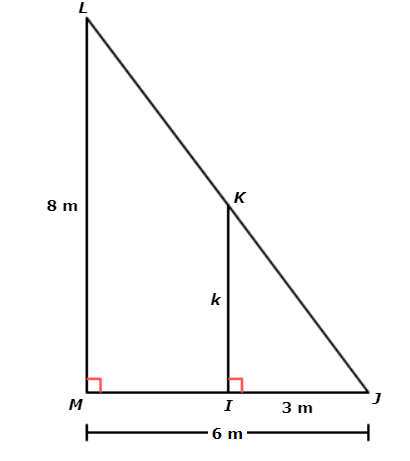
Write your answer as a whole number or a decimal. Do not round.
k = _______ metres
The original diagram included a smaller triangle inside a larger triangle. Redraw them as separate triangles.
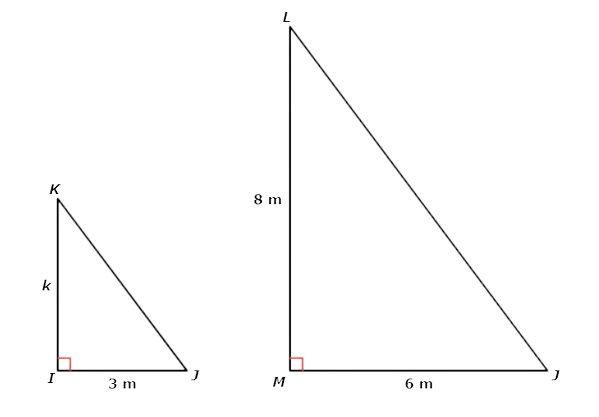
△IJK is similar to △MJL because all three pairs of corresponding angles are congruent.
One pair of corresponding side lengths is MJ and IJ . Together they form the fraction MJ / IJ .
Another pair of corresponding side lengths is LM and KI. Together they form the fraction LM / KI .
In both fractions, the numerator comes from △MJL and the denominator comes from △IJK .Since the triangles are similar, you can use the fractions to set up a proportion and solve for K.
MJ / IJ = LM / KI
6 / 3 = 8 / K Plug in the side lengths
6 / 3 (3k) = 8 / k (3k) Multiply both sides by 3k
6 k = 8 . 3 Simplify
6k = 24 Simplify
6k ÷ 6 = 24 ÷ 6 Divide both sides by 6
k = 4
The missing length is 4 metres.
Let’s practice!

