Side lengths and angle measures in similar figures
Key Notes :
Two polygons are similar if and only if their corresponding angles are congruent and their corresponding sides are proportional.
Learn with an example
△VWX~△STR. Find RT.
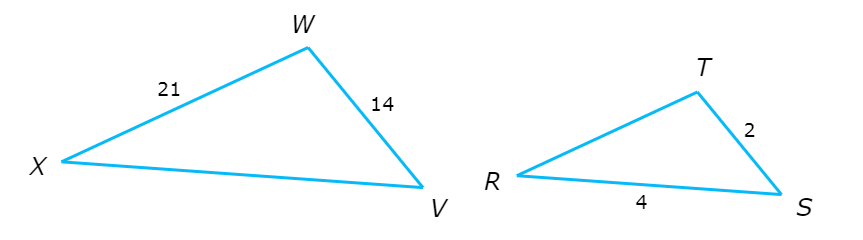
RT = _________
Use the fact that VWX is similar to STR to write proportions and solve for RT.
△VWX ~ △STR
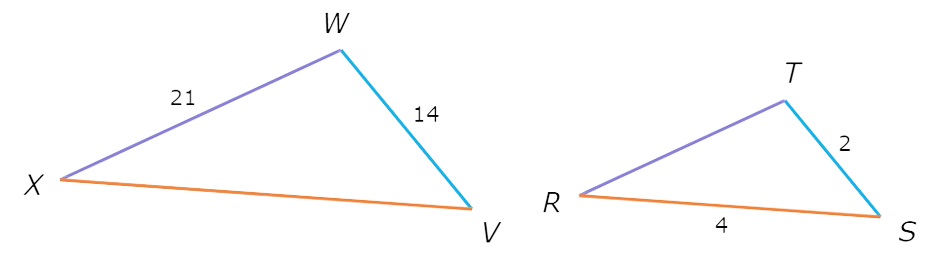
To start, find two corresponding sides whose lengths are given: VW=14 and ST=2. Now write the proportions
Write a proportion to solve for RT . Use VW , ST , RT , and its corresponding side WX.
VW / ST = WX / RT Definition of similarity
14 / 2 = 21 / RT Plug in VW=14, ST=2 and WX=21
7 = 21 / RT Simplify
7 . RT = 21 Multiply both sides by RT
RT = 3 Divide both sides by 7
So, RT=3.
△BCD ~ △JHI. Find BC.

BC = ______
Use the fact that BCD is similar to JHI to write proportions and solve for BC.
△BCD~△JHI
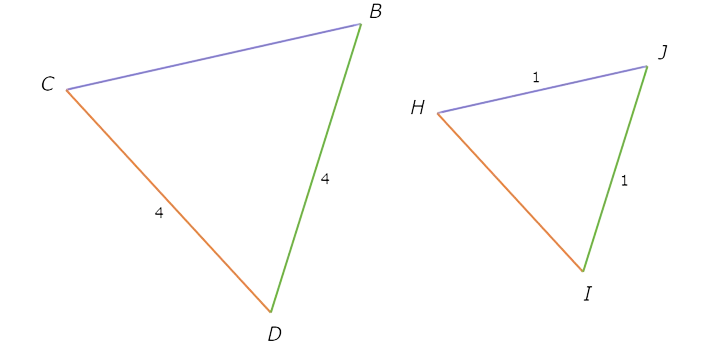
To start, find two corresponding sides whose lengths are given: BD=4 and IJ=1. Now write the proportions.
Write a proportion to solve for BC . Use BD , IJ , BC , and its corresponding side HJ.
BD / IJ = BC / HJ Definition of similarity
4 / 1 = BC / 1 Plug in BD=4, IJ=1 and HJ=1
4 = BC Simplify
So , BC = 4.
△WXY ~ △EFD. What is ∠W?
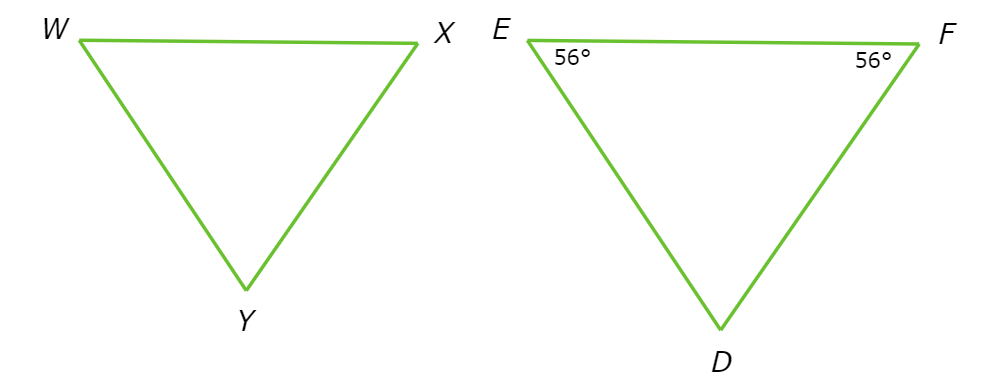
∠W = ______ °
∠W is not given, but the measure of its corresponding angle—∠E—is.
△WXY ~ △EFD
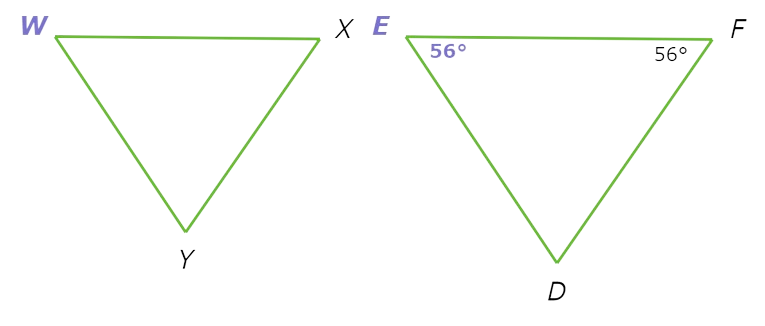
So, ∠W=∠E=56°.
Let’s practice!

