Similarity statements
Key Notes :
Two triangles are similar if and only if corresponding angles are congruent and corresponding sides are proportional.
Learn with an example
The two triangles below are similar.
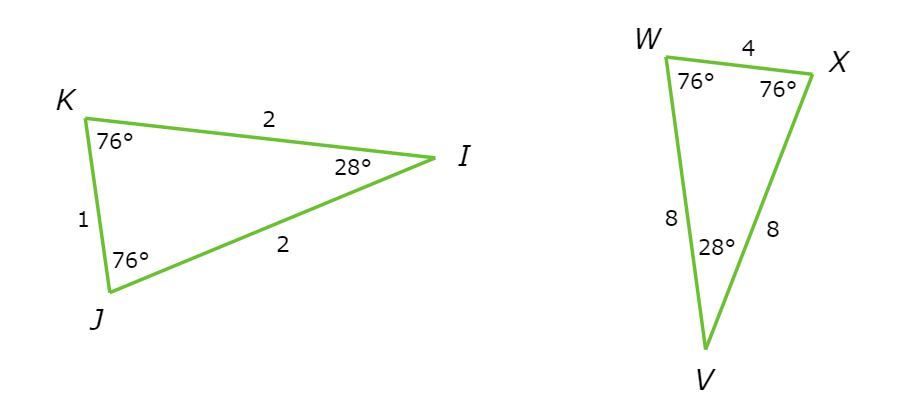
Complete the similarity statement.
△ IJK ~ △ ______
You know these triangles are similar, but you don’t know a specific similarity statement. Look at the triangles to see how they correspond.
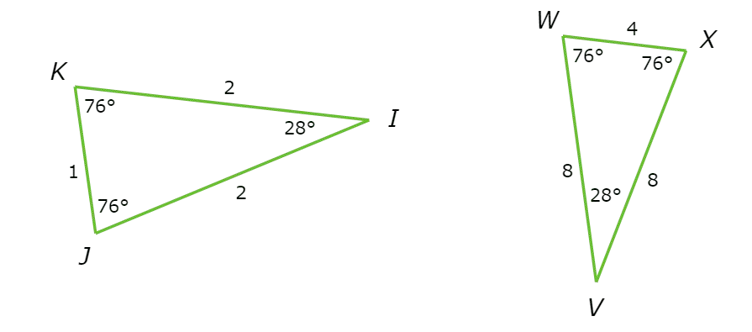
You can pair the angles so that corresponding angles are congruent.
∠I ≅ ∠V
∠J ≅ ∠W
∠K ≅ ∠X
Next, look at the sides. All the corresponding sides are proportional.
IJ / VW = 2/8 = 1/4
JK / WX = 1/4
IK / VX = 2/8 = 1/4
Since the corresponding angles are congruent and the corresponding sides are proportional,
△IJK ~ △VWX.
The two polygons below are similar.
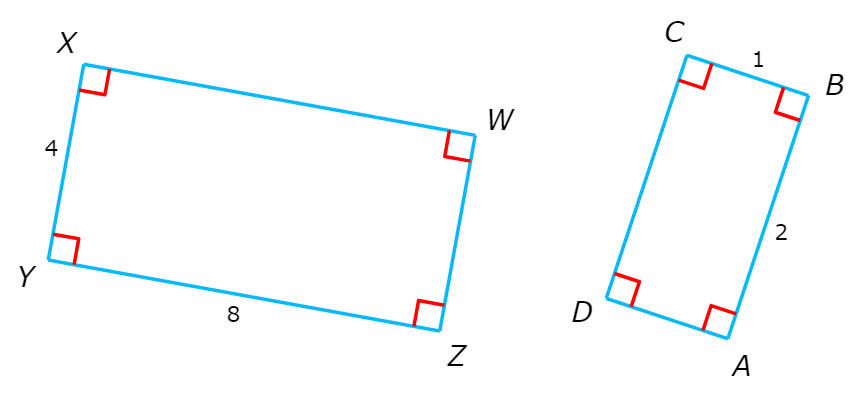
Complete the similarity statement.
WXYZ ~ ______
Since WXYZ is a rectangle, its opposite sides are congruent. So, WX = YZ = 8 and XY = WZ = 4 .
Since ABCD is a rectangle, its opposite sides are also congruent. So, AB = CD = 2 and BC = AD = 1.
You know these polygons are similar, but you don’t know a specific similarity statement. Look at the polygons to see how they correspond.
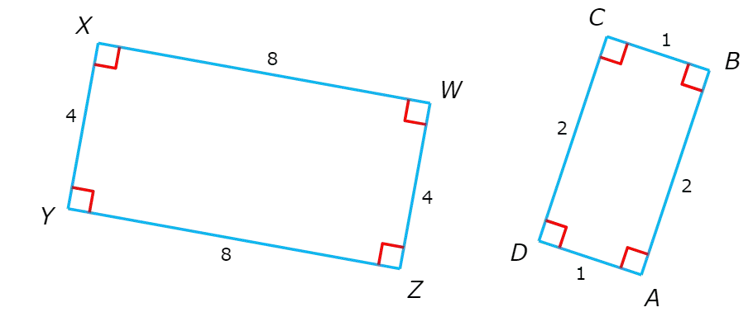
Pair the angles so that the shorter sides and longer sides in each rectangle will correspond to each other. Corresponding angles will be congruent because all the angles are right angles:
∠W ≅ ∠A
∠X ≅ ∠B
∠Y ≅ ∠C
∠Z ≅ ∠D
Next, look at the sides. All the corresponding sides are proportional.
WX / AB = 8/2 = 4
XY / BC = 4/1 = 4
YZ / CD = 8/2 = 4
WZ / AD = 4/1 = 4
Since the corresponding angles are congruent and the corresponding sides are proportional, WXYZ ~ ABCD.
The two triangles below are similar.
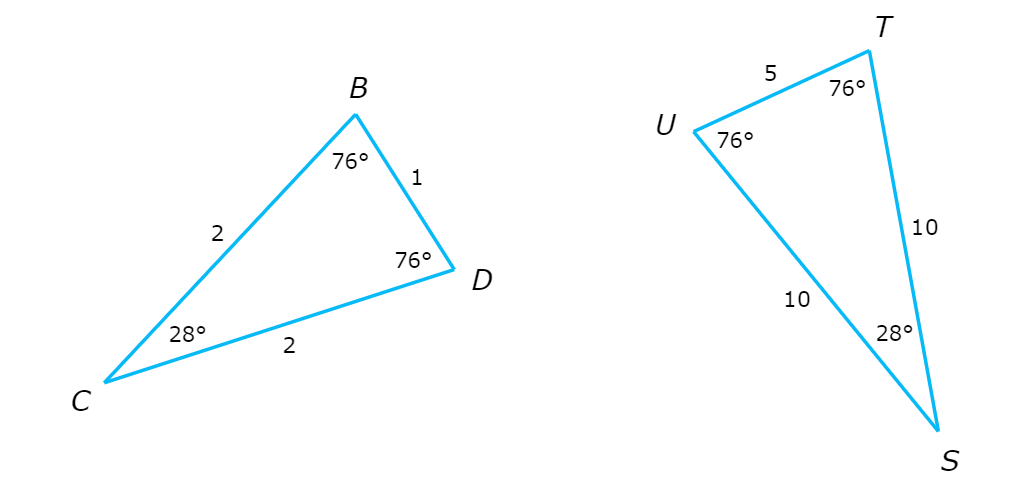
Complete the similarity statement.
△BCD ~ △ _____
You know these triangles are similar, but you don’t know a specific similarity statement. Look at the triangles to see how they correspond.
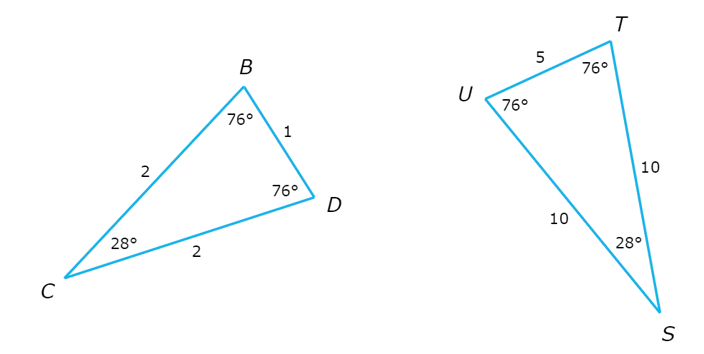
You can pair the angles so that corresponding angles are congruent.
∠B ≅ ∠U
∠C ≅ ∠S
∠D ≅ ∠T
Next, look at the sides. All the corresponding sides are proportional.
BC / SU = 2/10 = 1/5
CD / ST = 2/10 = 1/5
BD / TU = 1/5
Since the corresponding angles are congruent and the corresponding sides are proportional, △BCD ~ △UST.
let’s practice!

