Similarity ratios
Key Notes :
If two triangles are similar, their similarity ratio is the ratio between a side length in the first triangle and the corresponding side length in the second triangle.
Learn with an example
△XYZ ~ △DEF.
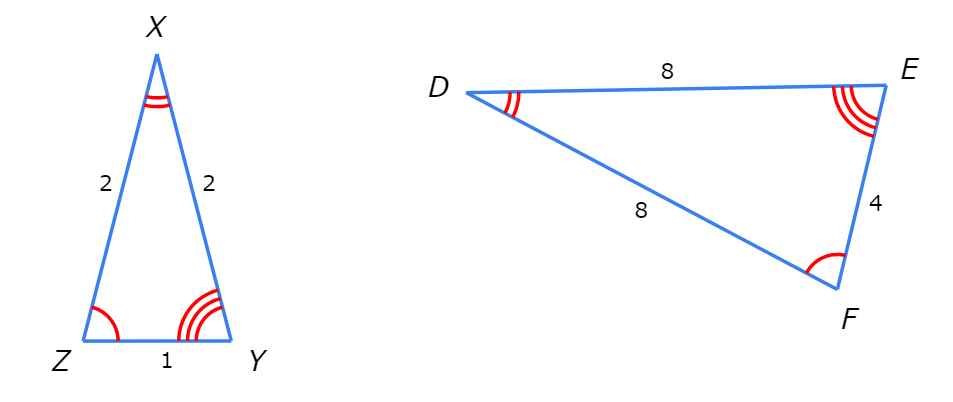
Find the ratio of a side length in △XYZ to its corresponding side length in △DEF
Simplify your answer and write it as a proper fraction, improper fraction, or whole number.
Choose any side in △XYZ and the corresponding side in △DEF . Then, find the ratio of the side lengths.
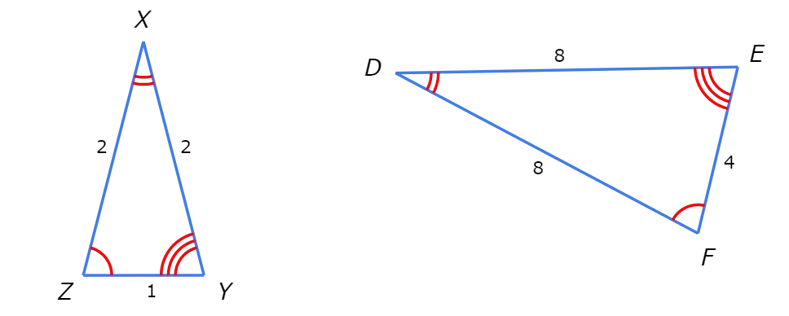
For example, you can use XY and DE .
XY / DE = 2/8 = 1/4
△QRS ~ △HFG.
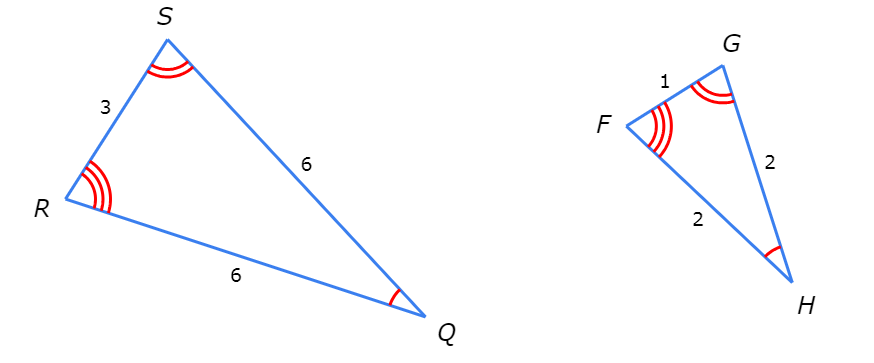
Find the ratio of a side length in △QRS to its corresponding side length in △HFG
Simplify your answer and write it as a proper fraction, improper fraction, or whole number.
Choose any side in △QRS and the corresponding side in △HFG . Then, find the ratio of the side lengths.
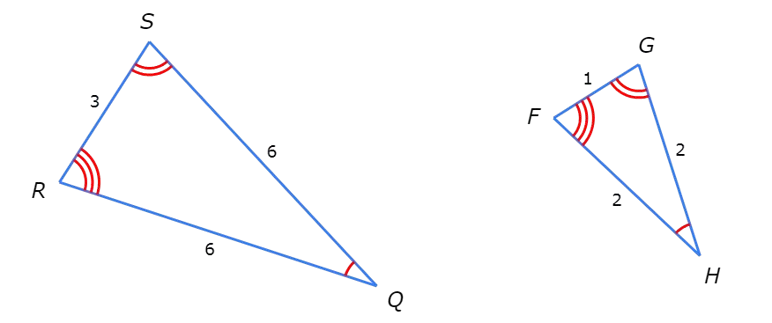
For example, you can use RS and FG .
RS / FG = 3/1 = 3.
△FGH ~ △UVW.
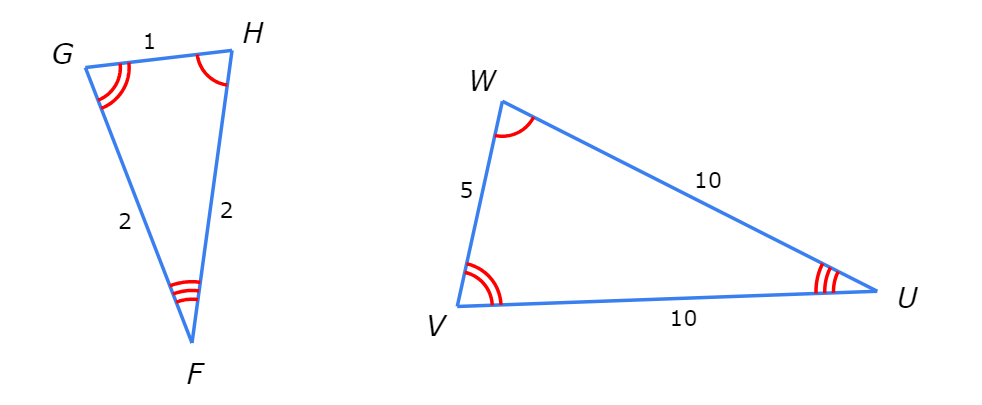
Find the ratio of a side length in △FGH to its corresponding side length in △UVW
Simplify your answer and write it as a proper fraction, improper fraction, or whole number.
Choose any side in △FGH and the corresponding side in △UVW . Then, find the ratio of the side lengths.
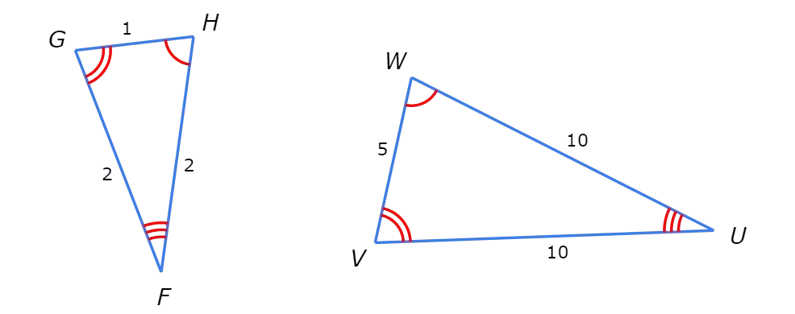
For example, you can use GH and VW.
GH / VW = 1/5.
Let’s practice!

