Identify similar figures
Key Notes :
Shapes are similar if their corresponding angles are all congruent and their corresponding sides are proportional.
Learn with an example
Are these shapes similar?
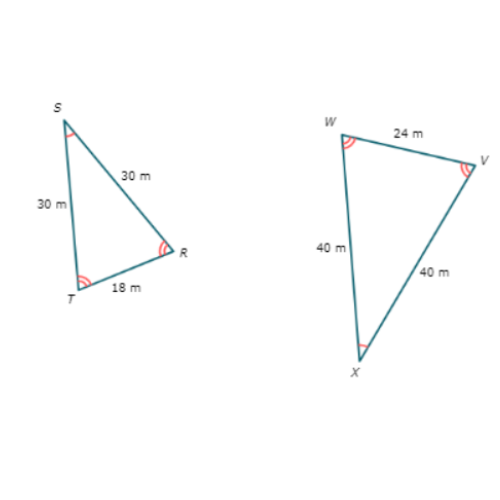
- Yes
- No
Look for the parts that appear to be corresponding. Reflect the second shape so that it matches the first shape.
First, see if the corresponding angles are all congruent.
T ≅ W
S ≅ X
R ≅ V
The corresponding angles are all congruent.
Next, see if the corresponding sides are proportional. Start by finding the lengths of all the sides.
TS and WX have a ratio of 30/40 , which is equivalent to 3/4.
SR and XV have a ratio of 30/40 , which is equivalent to 3/4.
RT and VW have a ratio of 18/24, which is equivalent to 3/4.
The ratios are all 3/4, so the corresponding sides are proportional.
Since the corresponding angles are all congruent and the corresponding sides are proportional, the shapes are similar.
Are these shapes similar?
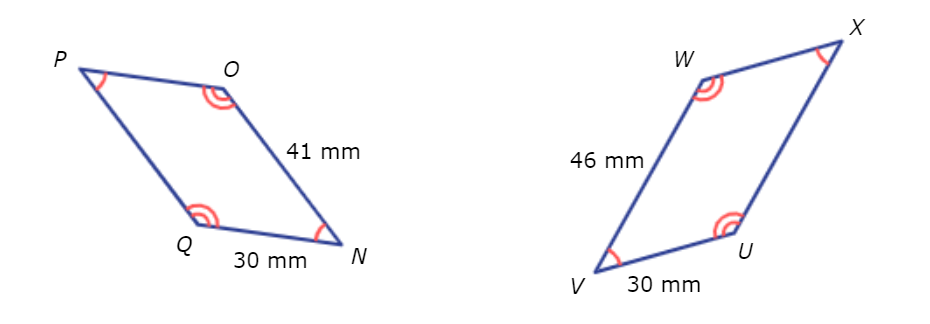
- Yes
- No
Look for the parts that appear to be corresponding. Reflect the second shape so that it matches the first shape.

First, see if the corresponding angles are all congruent.
∠Q ≅ ∠W
∠N ≅ ∠X
∠0 ≅ ∠U
∠P ≅ ∠V
The corresponding angles are all congruent.
Next, see if the corresponding sides are proportional. Start by finding the lengths of all the sides.
QNOP is a parallelogram. The opposite sides are congruent. QN is 30 mm and PQ is 41 mm.
WXUV is also a parallelogram. The opposite sides are congruent. WX is 30 mm and XU is 46 mm.
QN and WX have a ratio of 30/30 , which is equivalent to 1/1 .
NO and XU have a ratio of 41/46 .
OP and UV have a ratio of 30/30 , which is equivalent to 1/1 .
PQ and VW have a ratio of 41/46 .
The ratios are not all the same, so the corresponding sides are not proportional.
Since the corresponding sides are not proportional, the shapes are not similar.
let’s practice!

