Triangle Inequality Theorem
Key Notes :
1. Definition:
- The Triangle Inequality Theorem states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
- This theorem can be written as:
- ( a + b > c )
- ( b + c > a )
- ( a + c > b )
- where (a), (b), and (c) are the lengths of the sides of the triangle.
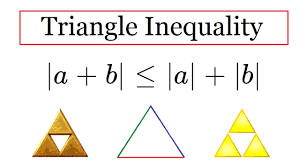
2. Explanation:
- The theorem ensures that a valid triangle can only be formed if the sum of any two sides is greater than the third side.
- This is because if one side is too long compared to the sum of the other two sides, it would prevent the sides from meeting to form a closed shape (a triangle).
3. Examples:
- Example 1:
- Consider a triangle with side lengths 3 cm, 4 cm, and 5 cm.
- Apply the Triangle Inequality:
- ( 3 + 4 > 5 ) (7 > 5, true)
- ( 3 + 5 > 4 ) (8 > 4, true)
- ( 4 + 5 > 3 ) (9 > 3, true)
- Since all inequalities hold, the sides can form a triangle.
- Example 2:
- Consider side lengths 2 cm, 5 cm, and 8 cm.
- Apply the Triangle Inequality:
- ( 2 + 5 > 8 ) (7 > 8, false)
- ( 2 + 8 > 5 ) (10 > 5, true)
- ( 5 + 8 > 2 ) (13 > 2, true)
- The first inequality fails, so these sides cannot form a triangle.
4. Converse of the Triangle Inequality Theorem:
- The converse is also true: If the sum of the lengths of any two sides of a triangle is greater than the third side, then a triangle exists.
5. Importance of the Theorem:
- Geometric Validity: Ensures that three given lengths can form a valid triangle.
- Applications in Problem Solving: This theorem helps determine whether a triangle is possible from given side lengths and is essential in triangle construction problems.
- Coordinate Geometry: The theorem can be applied to check if three points in the coordinate plane can form a triangle by calculating the distances between the points.
If 0≤a≤b≤c, then a, b, and c are the side lengths of a triangle if and only if
Learn with an example
Can the sides of a triangle have lengths 1, 6, and 9?
First, put the three numbers in order from smallest to largest: a=1, b=6, and c=9.
Now check whether a+b>c. Since 1+6=7, it is false that 1+6>9. So, these are not the side lengths of a triangle.
Can the sides of a triangle have lengths 1, 2, and 3?
First, put the three numbers in order from smallest to largest: a=1, b=2, and c=3.
Now check whether a+b>c. Since 1+2=3, it is false that 1+2>3. So, these are not the side lengths of a triangle.
Can the sides of a triangle have lengths 3, 6, and 8?
First, put the three numbers in order from smallest to largest: a=3, b=6, and c=8.
Now check whether a+b>c. Since 3+6=9, it is true that 3+6>8. So, these are the side lengths of a triangle.
Can the sides of a triangle have lengths 3, 6, and 10?
First, put the three numbers in order from smallest to largest: a=3, b=6, and c=10.
Now check whether a+b>c. Since 3+6=9, it is false that 3+6>10. So, these are not the side lengths of a triangle.
Can the sides of a triangle have lengths 2, 3, and 5?
First, put the three numbers in order from smallest to largest: a=2, b=3, and c=5.
Now check whether a+b>c. Since 2+3=5, it is false that 2+3>5. So, these are not the side lengths of a triangle.
Can the sides of a triangle have lengths 2, 7, and 10?
First, put the three numbers in order from smallest to largest: a=2, b=7, and c=10.
Now check whether a+b>c. Since 2+7=9, it is false that 2+7>10. So, these are not the side lengths of a triangle.
Can the sides of a triangle have lengths 1, 10, and 10?
First, put the three numbers in order from smallest to largest: a=1, b=10, and c=10.
Now check whether a+b>c. Since 1+10=11, it is true that 1+10>10. So, these are the side lengths of a triangle.
Let’s practice!

