Angle-side relationships in triangles
Key Notes :
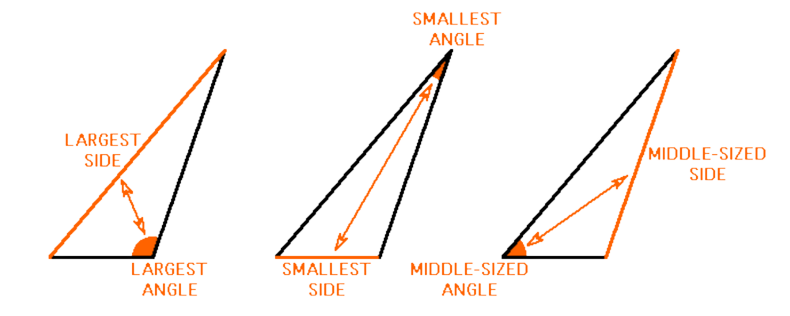
In a triangle, one side is longer than another if and only if its opposite angle is greater than the other’s.
Relationship between sides and angles
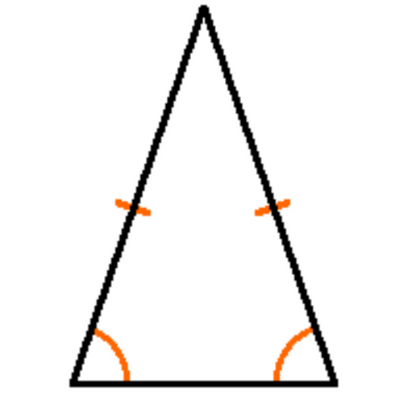
If two sides are congruent (equal in measure), then the corresponding two angles will be congruent (equal in measure).
Alternately, if two angles are congruent (equal in measure), then the corresponding two sides will be congruent (equal in measure).
Learn with an example
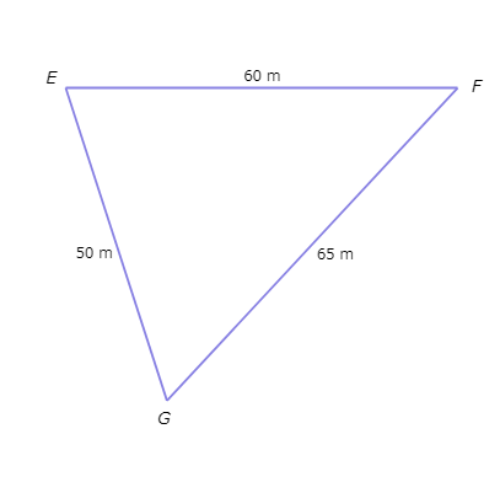
Find the largest angle of △EFG.
∠_____
The side lengths are EG=50 metres, EF=60 metres, and FG=65 metres. Since 50<60<65, EG<EF<FG.
Their opposite angles are in the same order, from smallest to largest:
∠F<∠G<∠E
So, the largest angle is ∠E.
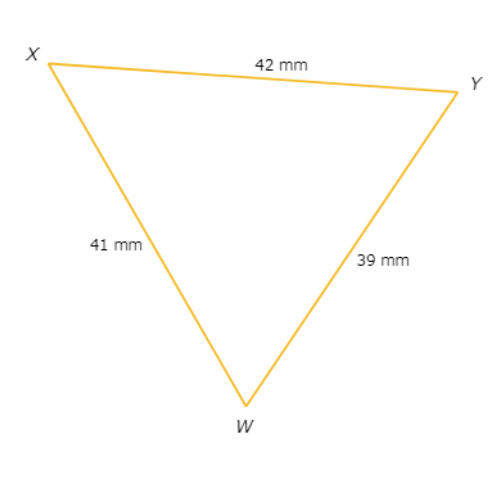
Find the Smallest angle of △WXY.
∠_____
The side lengths are WY=39 millimetres, WX=41 millimetres, and XY=42 millimetres. Since 39<41<42, WY<WX<XY.
Their opposite angles are in the same order, from smallest to largest:
∠X<∠Y<∠W
So, the smallest angle is ∠X.
Find the Smallest side of △IJK.
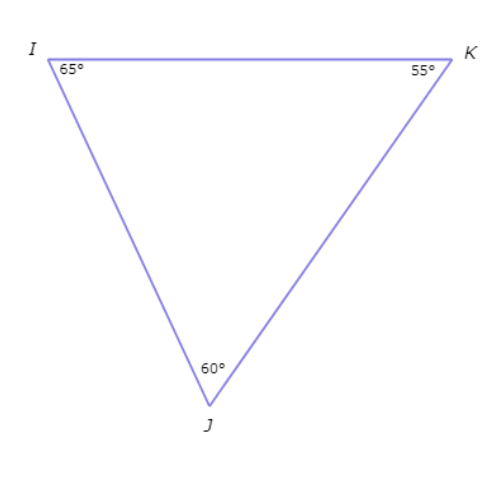
_____
Put the angles in order. Since 55°<60°<65°,∠K <∠J <∠I.
Their opposite sides are in the same order, from smallest to largest:
IJ<IK<JK
So, the smallest side is IJ.
let’s practice!

