Identify medians, altitudes, angle bisectors and perpendicular bisectors
Key Notes :
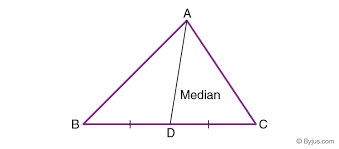
1. Median of a Triangle:
- Definition: A median is a line segment drawn from a vertex of the triangle to the midpoint of the opposite side.
- Key Properties:
- Every triangle has three medians, one from each vertex.
- The medians intersect at a point called the centroid. The centroid divides each median into two parts, with the longer part being twice the shorter part.
- The centroid is the center of mass or balance point of the triangle.
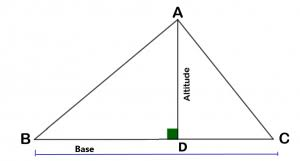
2. Altitude of a Triangle:
- Definition: An altitude is a perpendicular line segment from a vertex to the opposite side (or the line containing the opposite side).
- Key Properties:
- Every triangle has three altitudes, one from each vertex.
- The altitudes meet at a point called the orthocenter.
- In a right-angled triangle, the two legs of the triangle are the altitudes.
- In an obtuse triangle, one of the altitudes will lie outside the triangle.
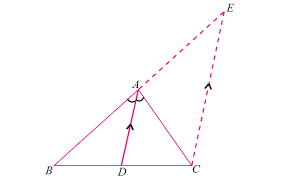
3. Angle Bisector of a Triangle:
- Definition: An angle bisector is a line segment that divides an angle of the triangle into two equal angles.
- Key Properties:
- Every triangle has three angle bisectors.
- The angle bisectors meet at a point called the incenter, which is equidistant from the sides of the triangle.
- The incenter is the center of the inscribed circle (the largest circle that can fit inside the triangle and touch all three sides).
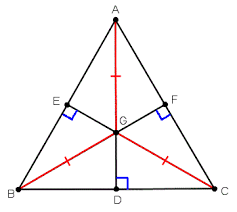
4. Perpendicular Bisector of a Triangle:
- Definition: A perpendicular bisector is a line that is perpendicular to a side of the triangle and divides that side into two equal parts.
- Key Properties:
- Every triangle has three perpendicular bisectors.
- The perpendicular bisectors meet at a point called the circumcenter, which is equidistant from the three vertices of the triangle.
- The circumcenter is the center of the circumscribed circle (the circle that passes through all three vertices of the triangle).
- In a right-angled triangle, the circumcenter lies at the midpoint of the hypotenuse.
- In an acute triangle, the circumcenter is inside the triangle, while in an obtuse triangle, it lies outside
5. Comparison of Properties:
- Centroid: Intersection of medians; divides medians in a 2:1 ratio.
- Orthocenter: Intersection of altitudes; can be inside, on, or outside the triangle.
- Incenter: Intersection of angle bisectors; center of the inscribed circle.
- Circumcenter: Intersection of perpendicular bisectors; center of the circumscribed circle.
Learn with an example
∠QRT ≅ ∠SRT.
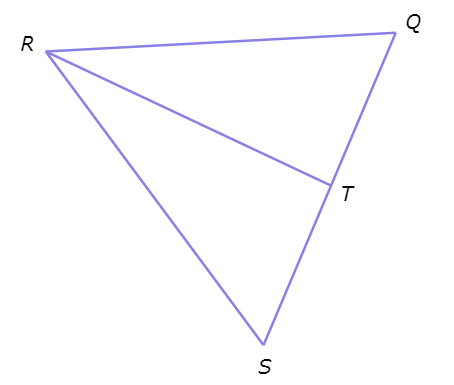
Which term describes RT ?
a ) median
b ) angle bisector
c ) perpendicular bisector
d ) altitude
∠QRT ≅ ∠SRT , so RT bisects ∠QRS.
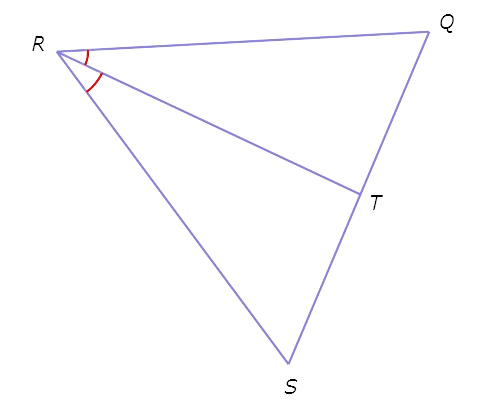
Therefore, RT is an angle bisector.
Also, since there is not enough information to know whether RT bisects QS or whether RT is perpendicular to QS, you cannot conclude that RT is a median, perpendicular bisector, or altitude.
∠FEG ≅ ∠GEH.
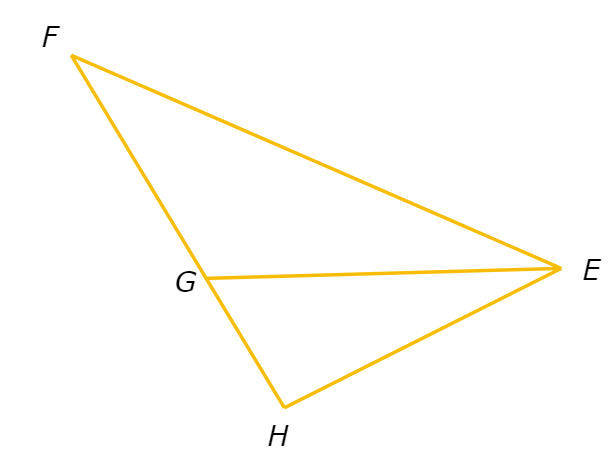
Which term describes EG ?
a ) angle bisector
b ) altitude
c ) perpendicular bisector
d ) median
∠FEG ≅ ∠GEH, so EG bisects ∠FEH.
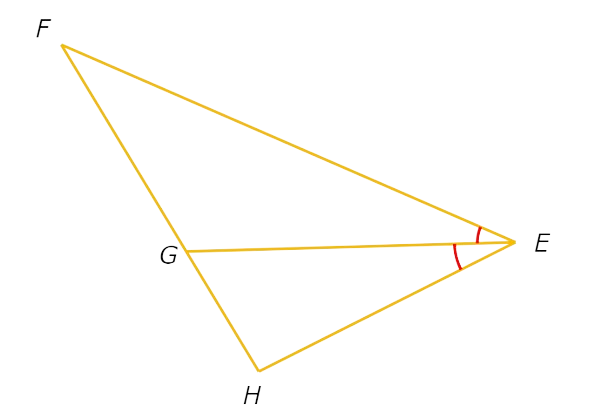
Therefore, EG is an angle bisector.
Also, since there is not enough information to know whether EG bisects FH or whether EG is perpendicular to FH, you cannot conclude that EG is a median, perpendicular bisector, or altitude.
∠GJH ≅ ∠HJI.
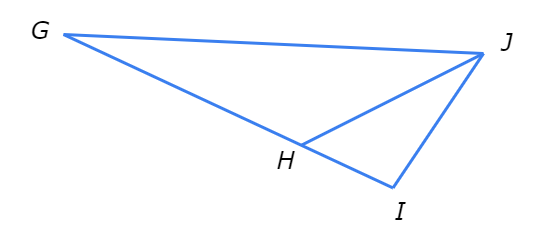
Which term describes JH ?
a ) median
b ) altitude
c ) perpendicular bisector
d ) angle bisector
∠GJH ≅ ∠HJI, so JH bisects ∠GJI.
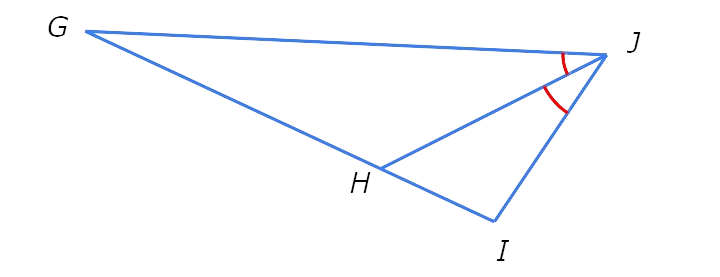
Therefore, JH is an angle bisector.
Also, since there is not enough information to know whether JH bisects GI or whether JH is perpendicular to GI , you cannot conclude that JH is a median, perpendicular bisector, or altitude.
Let’s practice!

