Triangles and bisectors
Key Notes :
📚 A point is equidistant from two lines if it is the same distance from them. The distance between a point and a line is the length of the segment perpendicular to the line from the point.
📚 The Angle Bisector Theorem states that a point is on the bisector of an angle if and only if it is in the interior of the angle and is equidistant from the sides of the angle.
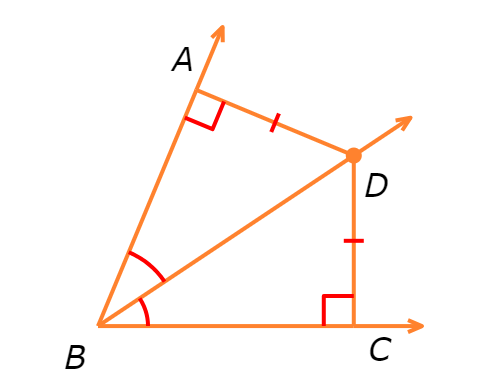
D is on the angle bisector of ∠ABC if and only if it is in the interior of ∠ABC and AD≅CD.
Learn with an example
✈️ What is TU?
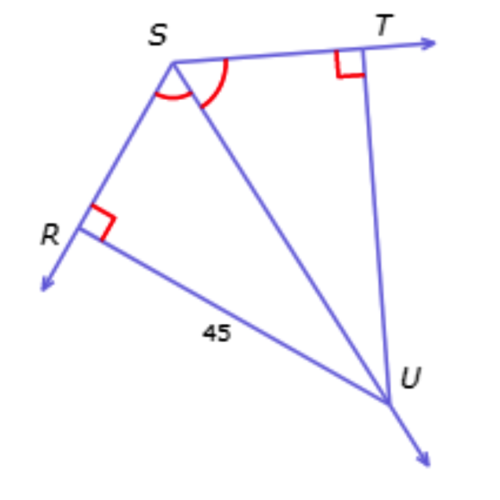
TU = _______
- Look at the diagram.
Since ∠RSU ≅ ∠TSU, SU bisects ∠RST.
Therefore, RU ≅ TU by the Angle Bisector Theorem.
So, TU = RU = 45.
✈️ What is DE?
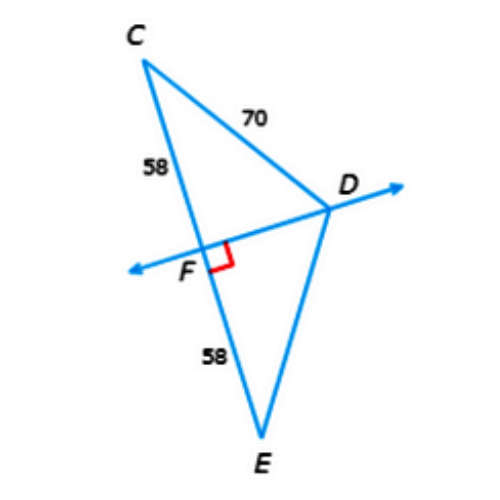
DE = ______
- Look at the diagram.
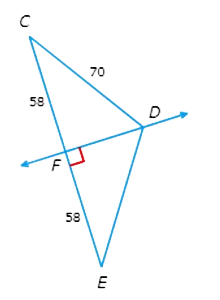
- Since ∠DFE is a right angle and CF=EF=58, DF is the perpendicular bisector of CE.
- Therefore, CD ≅ DE by the Perpendicular Bisector Theorem.
- So, DE=CD=70.
If RS ≅ ST and TU = 58, What is RT ?
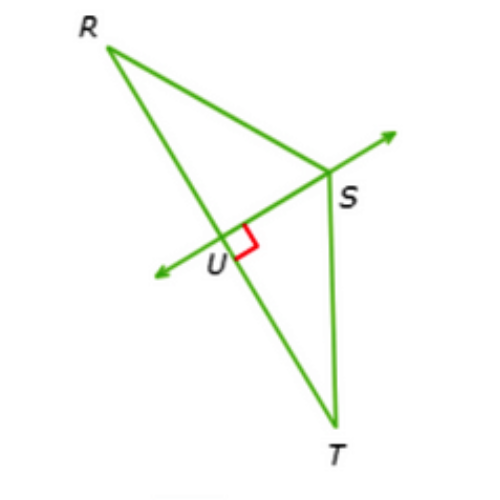
RT = ________
Label the diagram with the information given in the question.
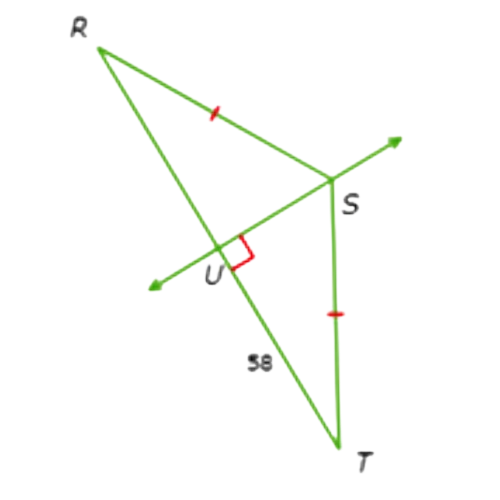
Since RS ≅ ST ,S is equidistant from the endpoints of RT. Therefore, S lies on the perpendicular bisector of RT by the Perpendicular Bisector Theorem.
Since S is on the perpendicular bisector of RT and ∠SUT is a right angle, SU is the perpendicular bisector of RT.
So, RU = TU = 58 and RT = 2 .58 = 116.
Let’s practice!

