Midsegments of triangles
Key Notes :
1. Definition of a Midsegment:
- A midsegment of a triangle is a line segment that connects the midpoints of two sides of the triangle.
- Each triangle has three midsegments, one for each pair of sides.
2. Properties of the Midsegment:
- Parallelism: The midsegment is parallel to the third side of the triangle (the side not connected by the midsegment).
- Length: The length of the midsegment is half the length of the third side.
- If the third side is denoted as ( AB ) and the midsegment connects the midpoints of ( AC ) and ( BC ), then ( \text{Midsegment} = \frac{1}{2} \times AB ).
- Divides the Triangle: The midsegment divides the triangle into two smaller triangles, each of which is similar to the original triangle by the Side-Angle-Side (SAS) Similarity Theorem.
3. Triangle Midsegment Theorem:
- This theorem states:
- A midsegment of a triangle is parallel to one side of the triangle and its length is half the length of that side.
- The theorem can be used to solve problems involving triangle side lengths and parallel lines.
Learn with an example
If TV=48, what is SW?
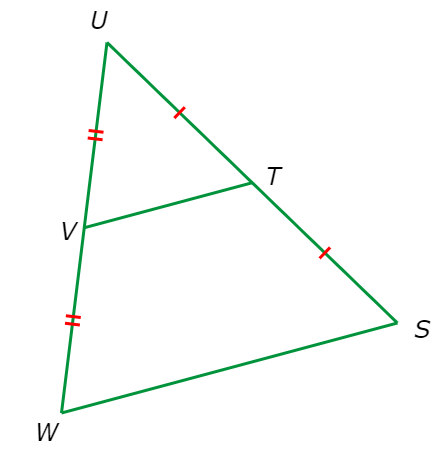
SW = ______
Since VW≅UV and ST≅TU,TV is a midsegment of △SUW.

So, TV is half of SW. In other words, SW is twice TV. Set SW equal to twice TV and solve for SW.
SW = 2 . TV
= 2(48) Plug in TV=48
= 96 Multiply
So, SW=96.
📚 If WX=66, what is VY?

VY = ______
Since XY≅YZ and VW≅VZ, VY is a midsegment of △WXZ.

So, VY is half of WX. Set VY equal to half of WX and solve for VY.
VY = WX / 2
= 66/2 Plug in WX=66
= 33 Divide
So, VY=33.
📚 If UV=22, what is WY?
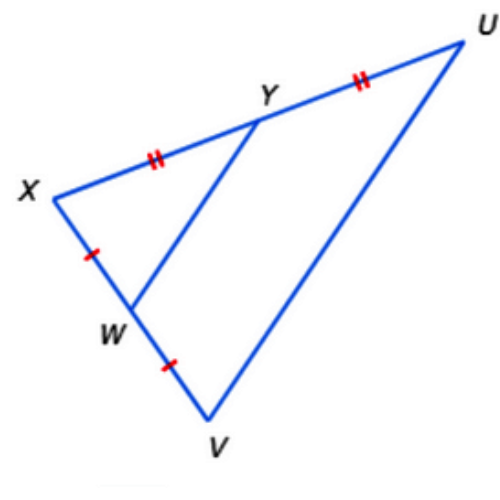
WY =_________
Since VW ≅ WX and UY ≅ XY, WY is a midsegment of △UVX.

So, WY is half of UY. Set WY equal to half of UY and solve for WY.
WY = UY / 2
= 22/2 Plug in UV=22
= 11 Divide
So, WY=11.
Let’s practice!

