Triangle angle-sum Theorem
Key Notes :
The sum of the interior angle measures of a triangle is 180°.
A triangle is the smallest polygon that has three sides and three interior angles. In this article, we are going to discuss the angle sum property
Angle Sum Property of a Triangle Theorem
In the given triangle, ∆ABC, AB, BC, and CA represent three sides. A, B and C are the three vertices and ∠ABC, ∠BCA and ∠CAB are three interior angles of ∆ABC.
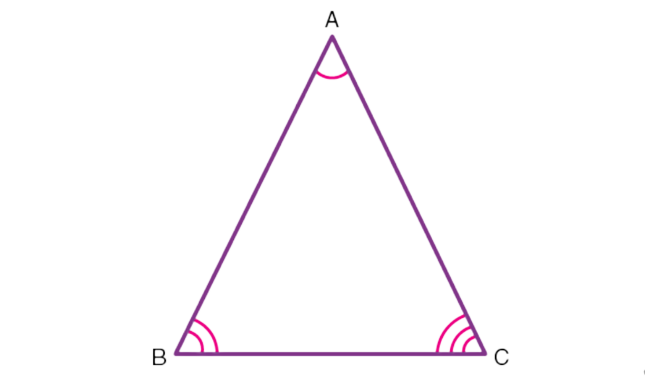
Angle sum property of triangle states that the sum of interior angles of a triangle is 180°.
Proof:
Consider a ∆ABC, as shown in the figure below. To prove the above property of triangles, draw a line PQ parallel to the side BC of the given triangle.
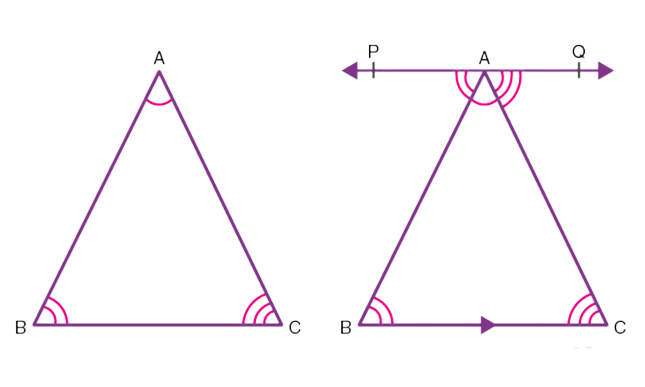
Since PQ is a straight line, it can be concluded that:
∠PAB + ∠BAC + ∠QAC = 180° ………(1)
Since PQ||BC and AB, AC are transversals,
Therefore, ∠QAC = ∠ACB (a pair of alternate angles)
Also, ∠PAB = ∠CBA (a pair of alternate angles)
Substituting the value of ∠QAC and ∠PAB in equation (1),
∠ACB + ∠BAC + ∠CBA= 180°
Thus, the sum of the interior angles of a triangle is 180°.
Learn with an example
The diagram shows a triangle
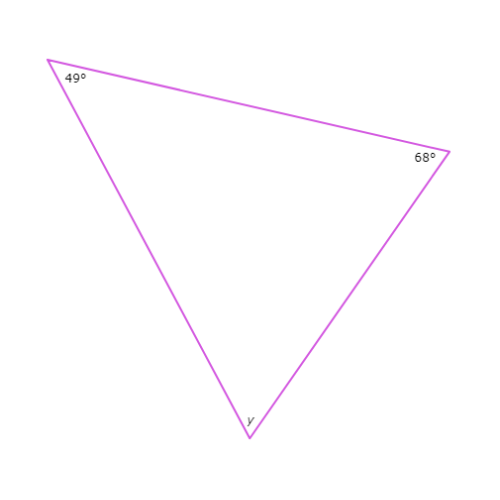
What is the value of Y ?
Y =_________°
First, look at the interior angle measures in the triangle.

Set the sum of the interior angle measures of the triangle equal to 180°. Solve for Y.
68° + Y + 49° = 180°
Y + 117° = 180° Combine like terms
Y = 63° Subtract 117° from both sides
So , Y = 63°
The diagram shows a triangle
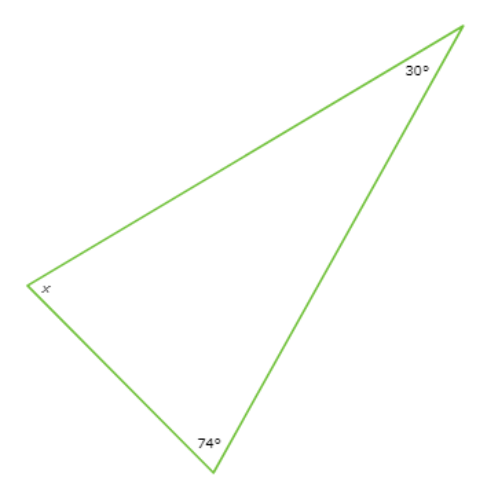
What is the value of X ?
Y =_________°
First, look at the interior angle measures in the triangle.
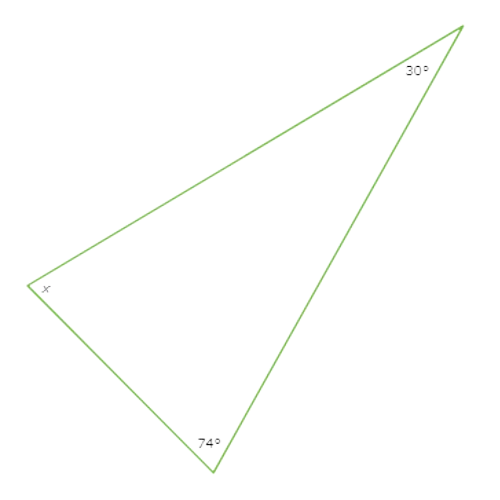
Set the sum of the interior angle measures of the triangle equal to 180°. Solve for X.
30° + 74° + X = 180°
X+ 104° = 180° Combine like terms
X = 76° Subtract 104° from both sides
So , X = 76°
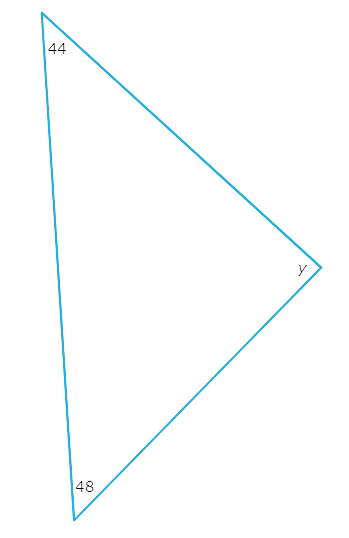
The diagram shows a triangle.
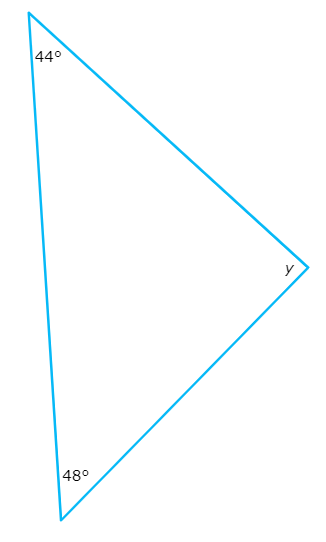
What is the value of Y ?
Y =_________°
First, look at the interior angle measures in the triangle.
Set the sum of the interior angle measures of the triangle equal to 180°. Solve for Y.
48° + Y + 44° = 180°
Y + 92° = 180° Combine like terms
Y = 88° Subtract 92° from both sides
So , Y = 88°
let’s practice!

