Classify triangles
Key Notes :
1. Classification by Sides:
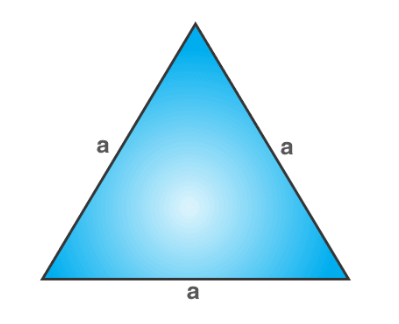
- Equilateral Triangle:
- Description: All three sides are equal, and all three interior angles measure 60°.
- Key Feature: Symmetrical in every way; all angles and sides are congruent.
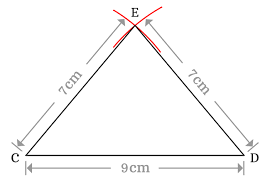
- Isosceles Triangle:
- Description: Two sides are of equal length, and the angles opposite these sides are equal.
- Key Feature: Often has two equal angles, making it visually symmetrical across one axis.
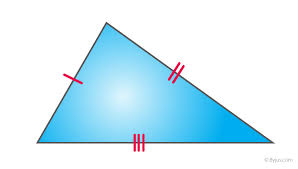
- Scalene Triangle:
- Description: All three sides have different lengths, and all three angles are different.
- Key Feature: No symmetry in sides or angles.
2. Classification by Angles:
- Acute Triangle:
- Description: All three interior angles are less than 90°.
- Key Feature: The sum of the three acute angles still equals 180°, but each individual angle is small.
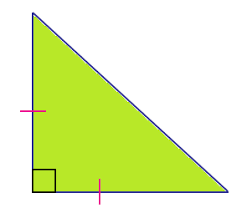
- Right-Angled Triangle:
- Description: One of the angles is exactly 90° (a right angle).
- Key Feature: The Pythagorean theorem applies, where the square of the hypotenuse (longest side) equals the sum of the squares of the other two sides: (a^2 + b^2 = c^2).
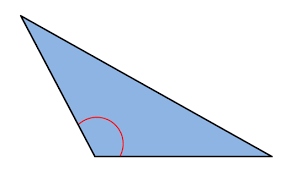
- Obtuse Triangle:
- Description: One of the angles is greater than 90°.
- Key Feature: The obtuse angle gives the triangle a wider, flatter shape.
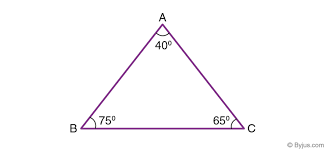
3. Sum of Interior Angles:
- In any triangle, the sum of the interior angles always equals 180°.
- Example: For an isosceles triangle with two equal angles of 45°, the third angle will be 90° (since 45° + 45° = 90°, and 180° – 90° = 90°).
Learn with an example
What kind of triangle is this?
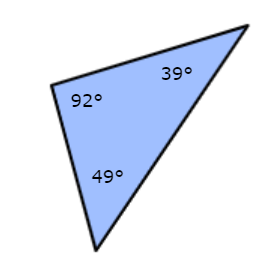
a ) Acute
b ) Right
c ) Obtuse
This triangle is an obtuse triangle. The 92° angle is greater than 90°.
A triangle has angle measurements of 74°, 47°, and 59°. Is this triangle equilateral?
a ) Yes
b ) No
This triangle is not equilateral. All 3 angles are different.
What kind of triangle is this?
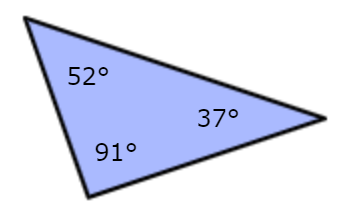
a ) Acute
b ) Right
c ) Obtuse
Look at this triangle:
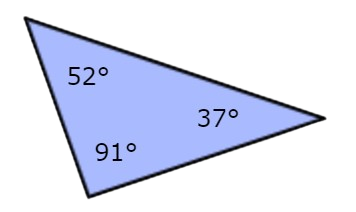
This triangle is an obtuse triangle. The 91° angle is greater than 90°.
let’s practice!

