Dilations: scale factor and classification
The scale factor of a dilation is the ratio of a length in the image after the dilation to the corresponding length in the original figure.
Learn with an example
The purple shape is a dilation of the black shape. What is the scale factor of the dilation?
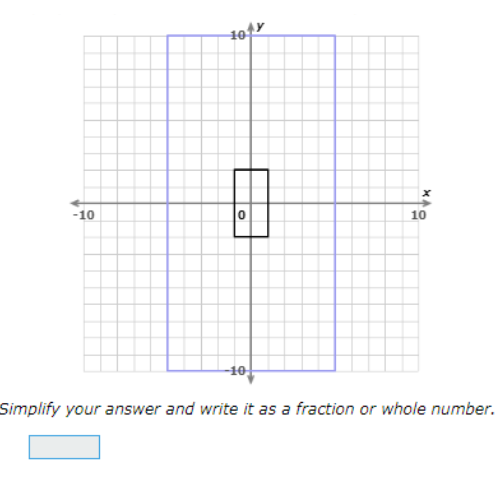
Find the length of one side in the original shape.
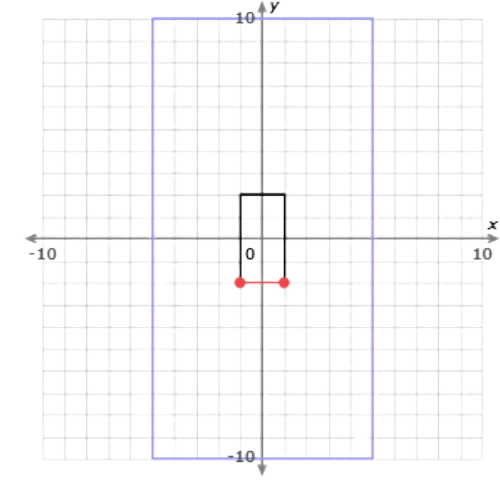
The side connects (–1, –2) and (1, –2). It is 2 units long.
Find the length of the corresponding side in the image.
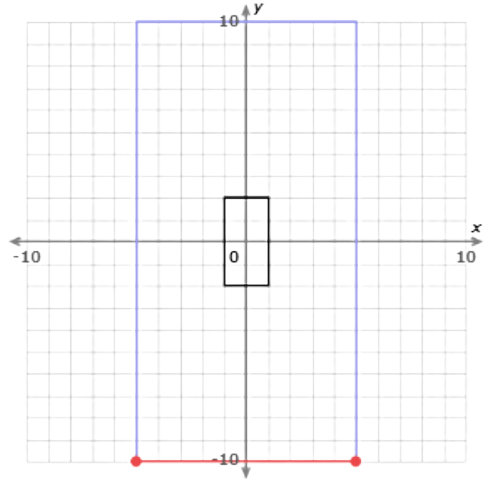
The side connects (–5, –10) and (5, –10). It is 10 units long.
Write the ratio of the length in the image to the length in the original figure.
10/2
Simplify the fraction.
10/2=5
The scale factor is 5.
The orange shape is a dilation of the black shape. Is it an enlargement or a reduction?
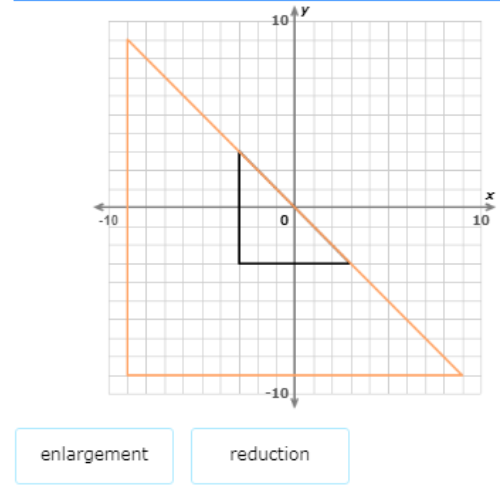
The orange shape is larger than the black shape. So, the dilation is an enlargement.
You can check your answer by finding the scale factor. Find the length of one side in the original shape.
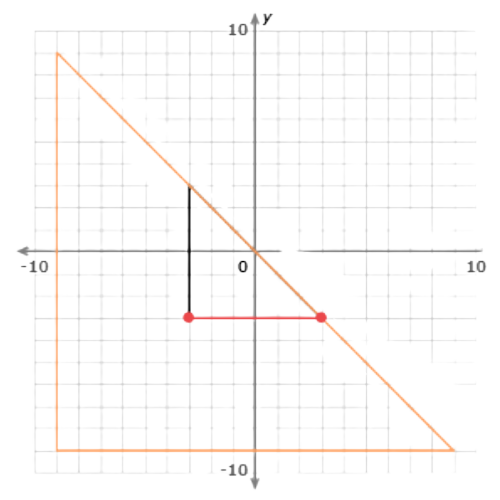
The side connects (–3, –3) and (3, –3). It is 6 units long.
Find the length of the corresponding side in the image.
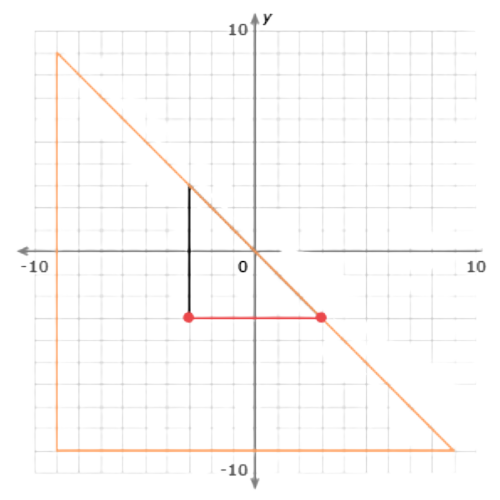
The side connects (–9, –9) and (9, –9). It is 18 units long.
Write the ratio of the length in the image to the length in the original figure.
18/6
Simplify the fraction.
18/6=3
The scale factor is 3. Since the scale factor is greater than 1, the dilation is an enlargement.
The green shape is a dilation of the black shape. Is it an enlargement or a reduction?
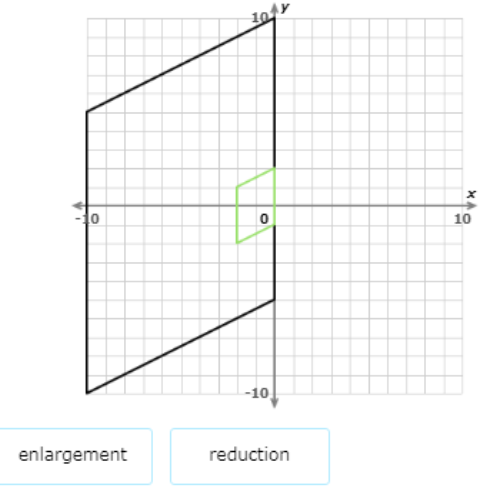
The green shape is smaller than the black shape. So, the dilation is a reduction.
You can check your answer by finding the scale factor. Find the length of one side in the original shape.
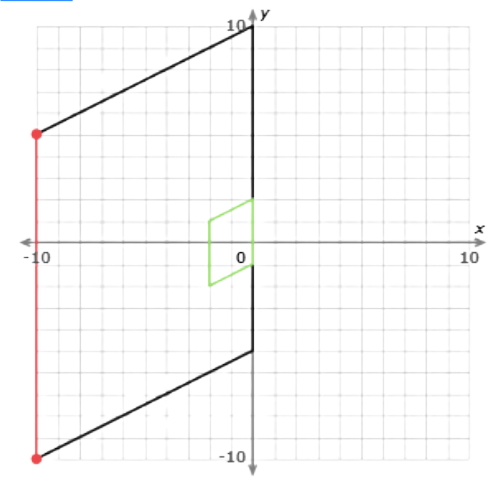
The side connects (–10, –10) and (–10, 5). It is 15 units long.
Find the length of the corresponding side in the image.
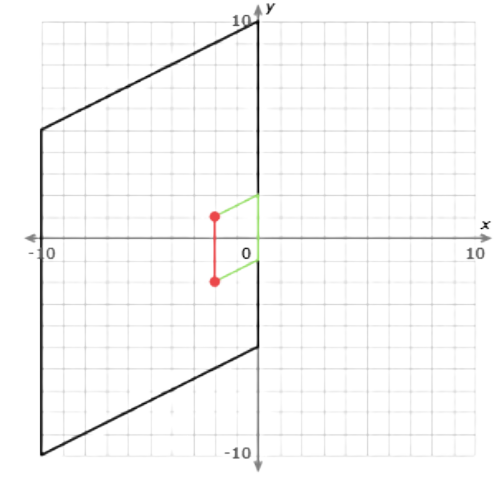
The side connects (–2, –2) and (–2, 1). It is 3 units long.
Write the ratio of the length in the image to the length in the original figure.
3/15
Simplify the fraction.
3/15=1/5
The scale factor is 1/5. Since the scale factor is greater than 1, the dilation is an enlargement.
let’s practice!

