Dilations: find the coordinates
A dilation enlarges or reduces a figure.
Learn with an example
Write the coordinates of the vertices after a dilation with a scale factor of 5, centred at the origin.
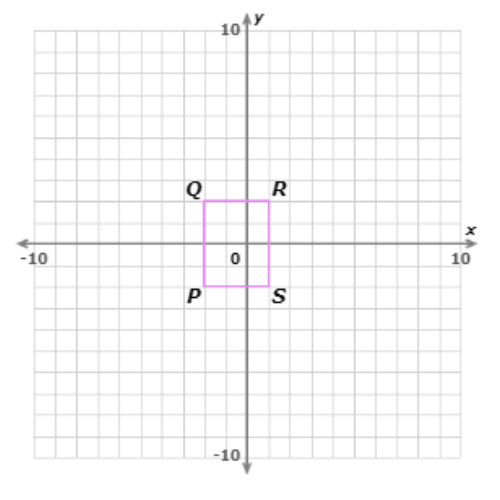

The scale factor of a dilation is the ratio of a length in the image to the corresponding length in the original figure.
This dilation is centred at the origin, so you can find the image by multiplying the x– and y-coordinates by the scale factor.
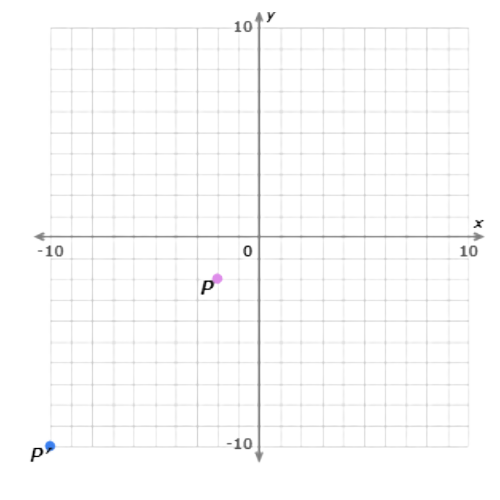
Multiply the coordinates of point P(–2, –2) by 5. The image is P′(–10, –10).
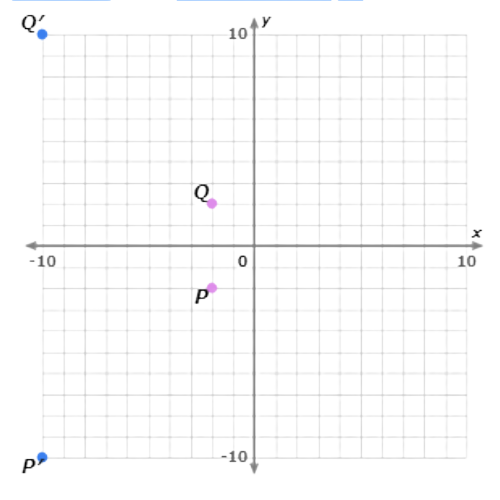
Now multiply the coordinates of point Q(–2, 2) by 5. The image is Q′(–10, 10).
Now multiply the coordinates of points R(1, 2) and S(1, –2) by 5. The images are R′(5, 10) and S′(5, –10).
The dilated points form a rectangle similar to PQRS.
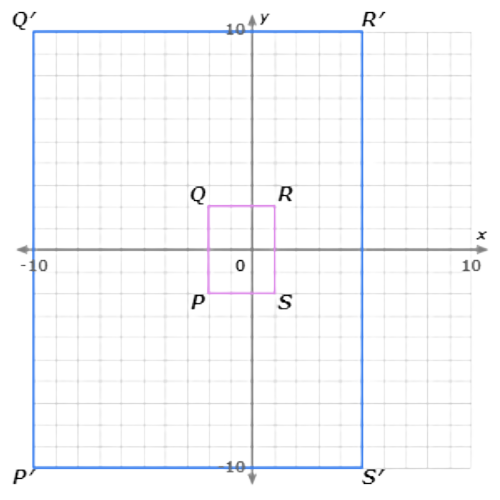
Write the coordinates of the vertices using arrow notation:
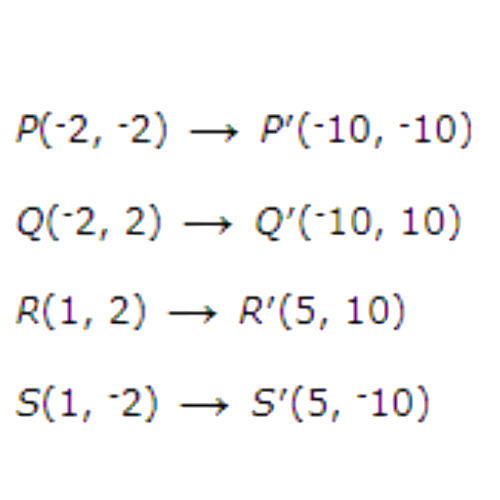
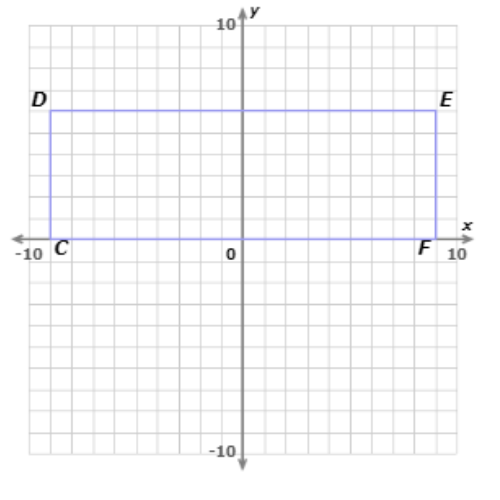
Write the coordinates of the vertices after adilation with a scale factor of 1/3,centred at the origin.

The scale factor of a dilation is the ratio of a length in the image to the corresponding length in the original figure.
This dilation is centred at the origin, so you can find the image by multiplying the x– and y-coordinates by the scale factor.
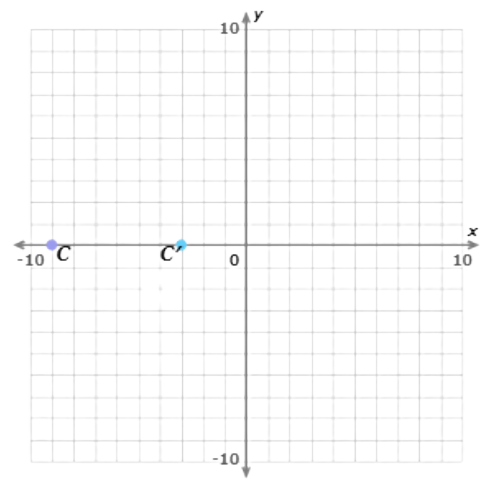
Multiply the coordinates of point C(–9, 0) by 1/3. The image is C′(–3, 0).
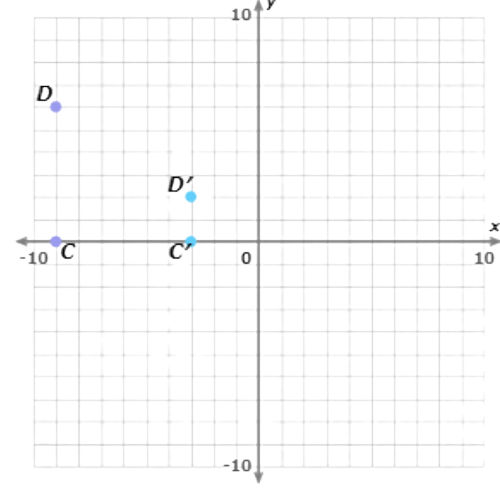
Now multiply the coordinates of point D(–9, 6) by 1/3.The image is D′(–3, 2).
Now multiply the coordinates of points E(9, 6) and F(9, 0) by 1/3.The images are E′(3, 2)and F′(3, 0).
The dilated points form a rectangle similar to CDEF.
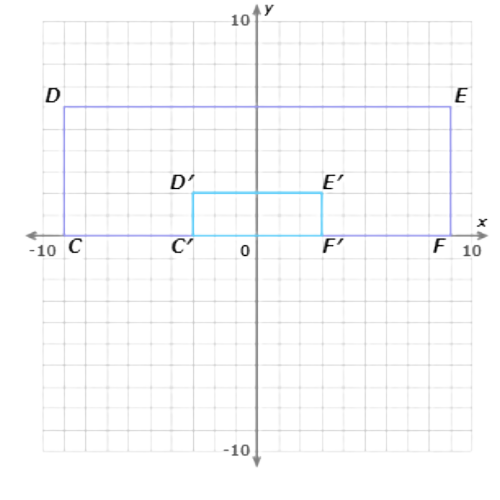
Write the coordinates of the vertices using arrow notation:
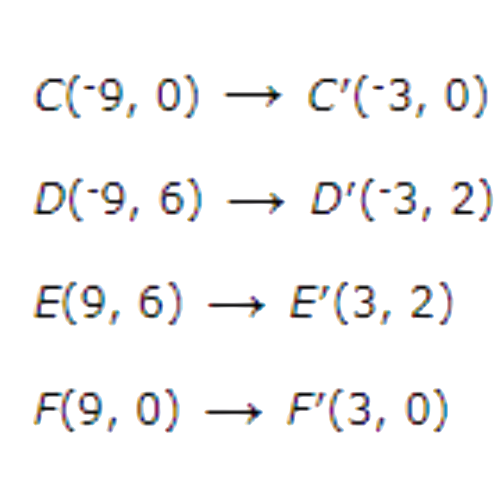
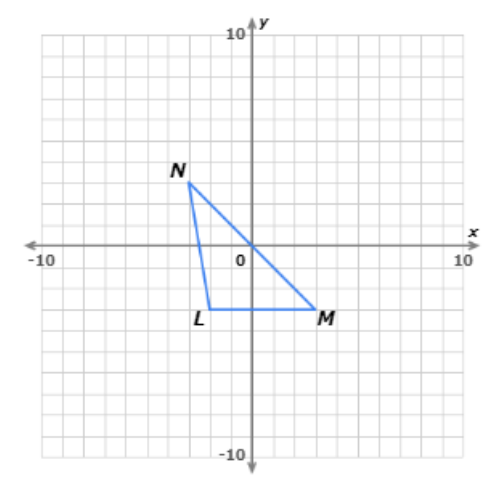
Write the coordinates of the vertices after a dilation with a scale factor of 3, centred at the origin.

The scale factor of a dilation is the ratio of a length in the image to the corresponding length in the original figure.
This dilation is centred at the origin, so you can find the image by multiplying the x– and y-coordinates by the scale factor.
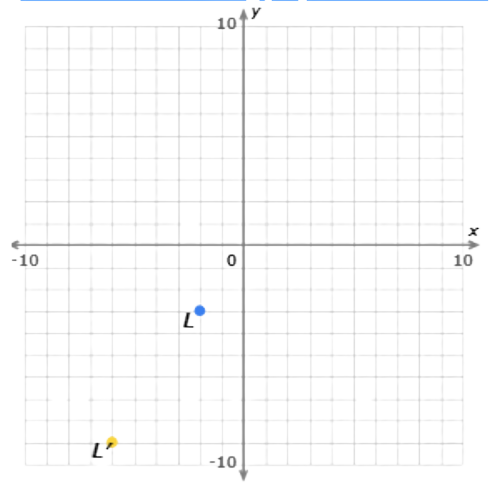
Multiply the coordinates of point L(–2, –3) by 3. The image is L′(–6, –9).
Now multiply the coordinates of point M(3, –3) by 3. The image is M′(9, –9).
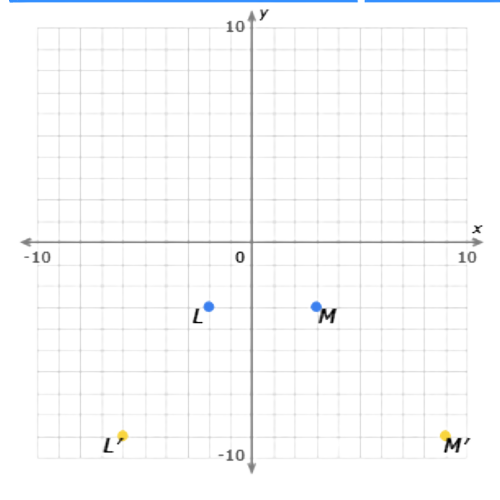
Now multiply the coordinates of point N(–3, 3) by 3. The image is N′(–9, 9).
The dilated points form a triangle similar to ![]() LMN.
LMN.
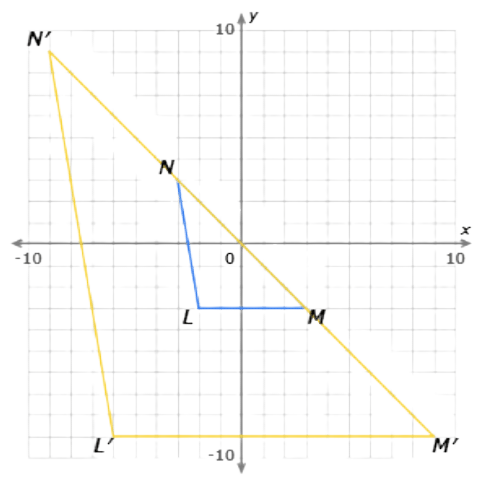
Write the coordinates of the vertices using arrow notation:
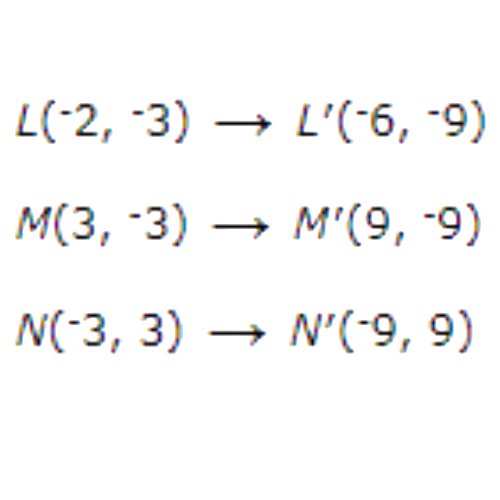
let’s practice!

