Compositions of congruence transformations: graph the image
Key Notes :
A glide reflection is the composition of a translation followed by a reflection across a line parallel to the direction of the translation.
The image of a point (x,y) translated h units horizontally and k units vertically is (x+h,y+k).
The image of a point (x,y) reflected across the x-axis is (x,–y).
Learn with an example
Graph the image of △ABC after the following glide reflection:
- Translation (x, y) ↦ (x+22, y)
- Reflection across the x-axis

First, translate △ABC.Use the transformation rule (x,y)↦(x+22,y)to find the image of each of its three vertices.
- A(–8, 4)↦A‘(14, 4)
- B(–14, 7)↦B‘(8, 7)
- C(–8, 10)↦C‘(14, 10)

Second, reflect △A‘B‘C‘across the x-axis.Use the transformation rule (x,y)↦(x,–y)to find the image of each of its three vertices.
- A‘(14, 4)↦A‘‘(14, –4)
- B‘(8, 7)↦B‘‘(8, –7)
- C‘(14, 10)↦C‘‘(14, –10)
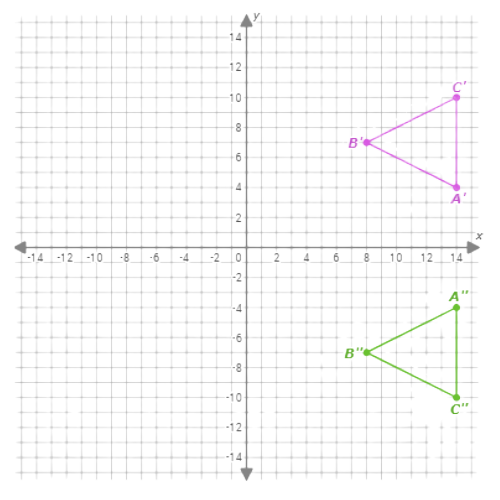
So, the image of △ABC after translating 22 units horizontally and 0 units vertically and reflecting across the x-axis is △A”B”C”.

Graph the image of △UVW after the following sequence of transformations:
- Rotation 270° anticlockwise around the origin
- Reflection across the y-axis
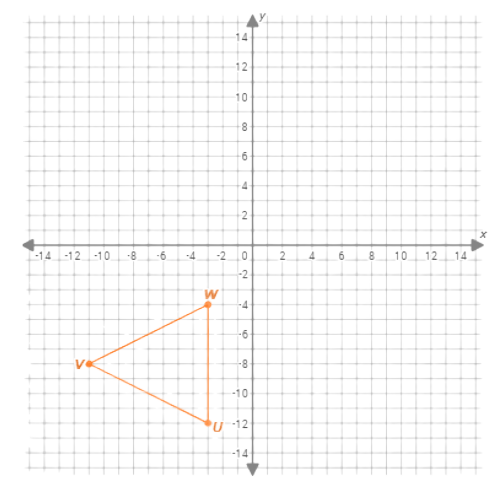
First, rotate △UVW 270° anticlockwise about the origin. Use the transformation rule (x,y)↦(y,–x)to find the image of each of its three vertices.
- U(–3, –12)↦U‘(–12, 3)
- V(–11, –8)↦V‘(–8, 11)
- W(–3, –4)↦W‘(–4, 3)
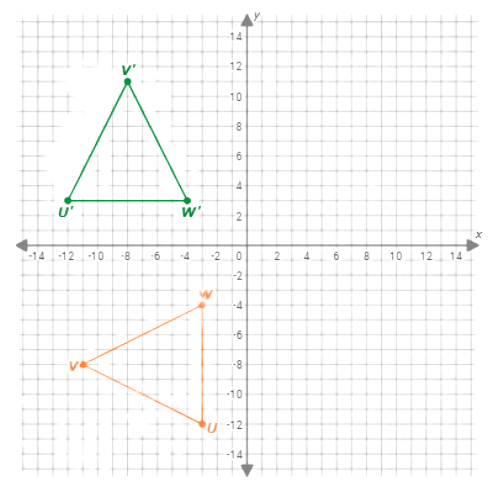
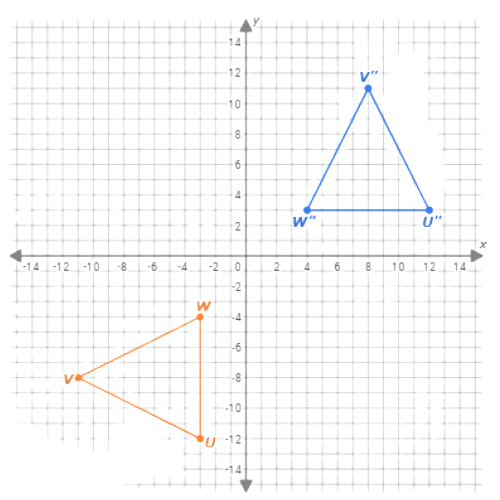
Second, reflect △U‘V‘W‘across the y-axis.Use the transformation rule (x,y)↦(–x,y)to find the image of each of its three vertices.
- U‘(–12, 3)↦U‘‘(12, 3)
- V‘(–8, 11)↦V‘‘(8, 11)
- W‘(–4, 3)↦W‘‘(4, 3)

So, the image of △UVW after rotating 270° anticlockwise around the origin and reflecting across the y-axis is △U”V”W”.
Graph the image of square FGHI after the following sequence of transformations:
- Translation (x, y) ↦ (x–17, y+20)
- Reflection across the y-axis
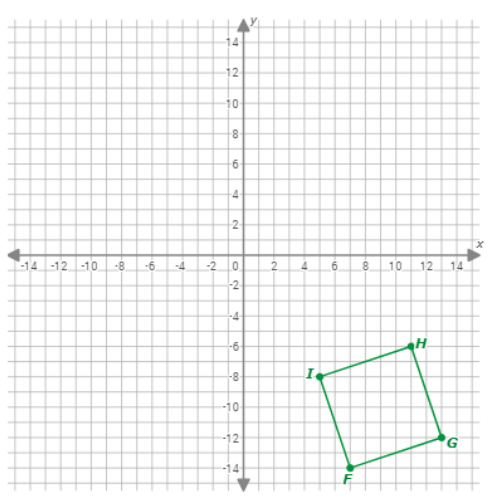
First, translate FGHI. Use the transformation rule (x,y)↦(x–17,y+20)to find the image of each of its four vertices.
- F(7, –14)↦F‘(–10, 6)
- G(13, –12)↦G‘(–4, 8)
- H(11, –6)↦H‘(–6, 14)
- I(5, –8)↦I‘(–12, 12)
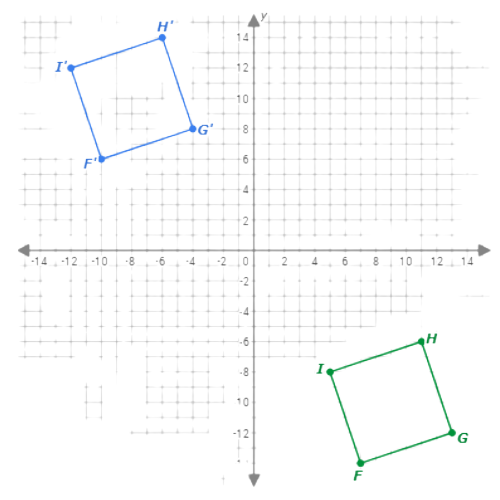
Second, reflect F‘G‘H‘I‘ across the y-axis.Use the transformation rule (x,y)↦(–x,y) to find the image of each of its four vertices.
- F‘(–10, 6)↦F‘‘(10, 6)
- G‘(–4, 8)↦G‘‘(4, 8)
- H‘(–6, 14)↦H‘‘(6, 14)
- I‘(–12, 12)↦I‘‘(12, 12)

So, the image of FGHI after translating –17 units horizontally and 20 units vertically and reflecting across the y-axis is F”G”H”I”.
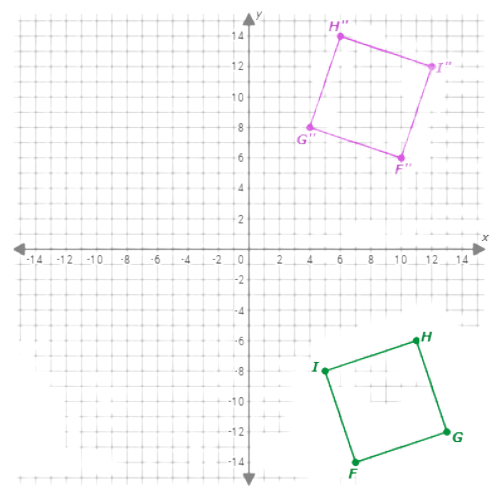
let’s practice!

