Congruence transformations
Key Notes :
A reflection flips a figure across a line to create a mirror image.
When a point is reflected across the line y=x the coordinates switch places.
Learn with an example
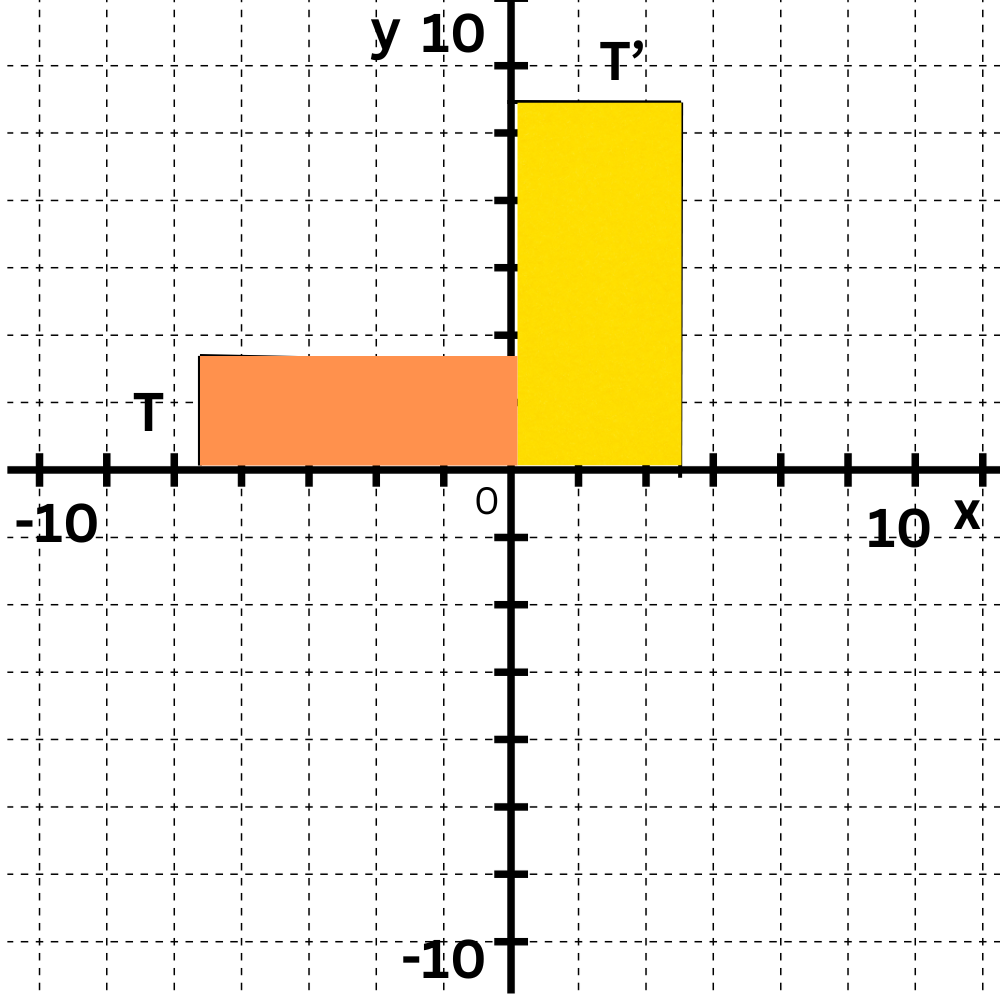
Write the coordinates of the vertices after a rotation 270° clockwise around the origin.
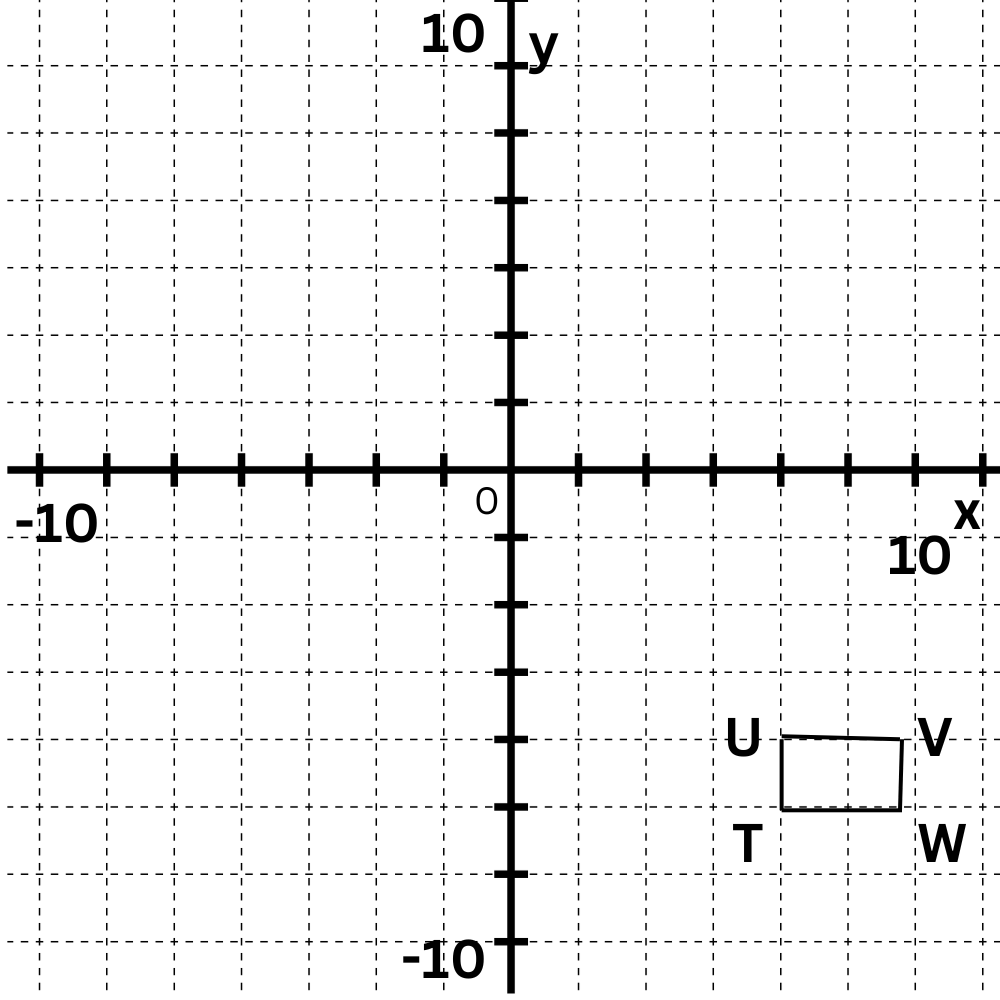
T (5,-7)——> T'(____ , ____)
U(5 ,-6)——>U'(____ , ____)
V(7 , -6)——>V'(____ , ____)
W(7 , 7)——>W'(____ , ____)
270°is 3/4 of a full turn . The rotation will turn the rectangle 3/4 of a full turn in the clockwise direction.
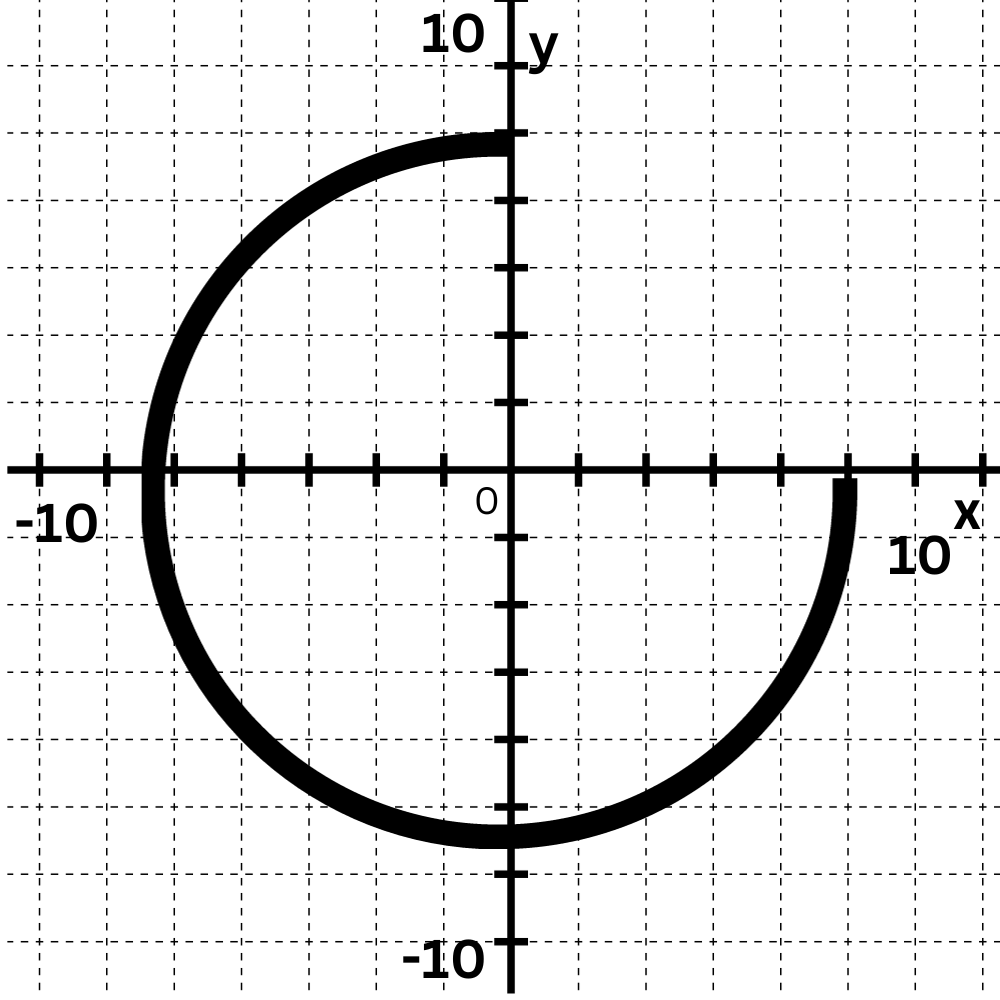
270° clockwise is the same as 90° anticlockwise. You can think of the rotation as 1/4 of a full turn in the anticlockwise direction.
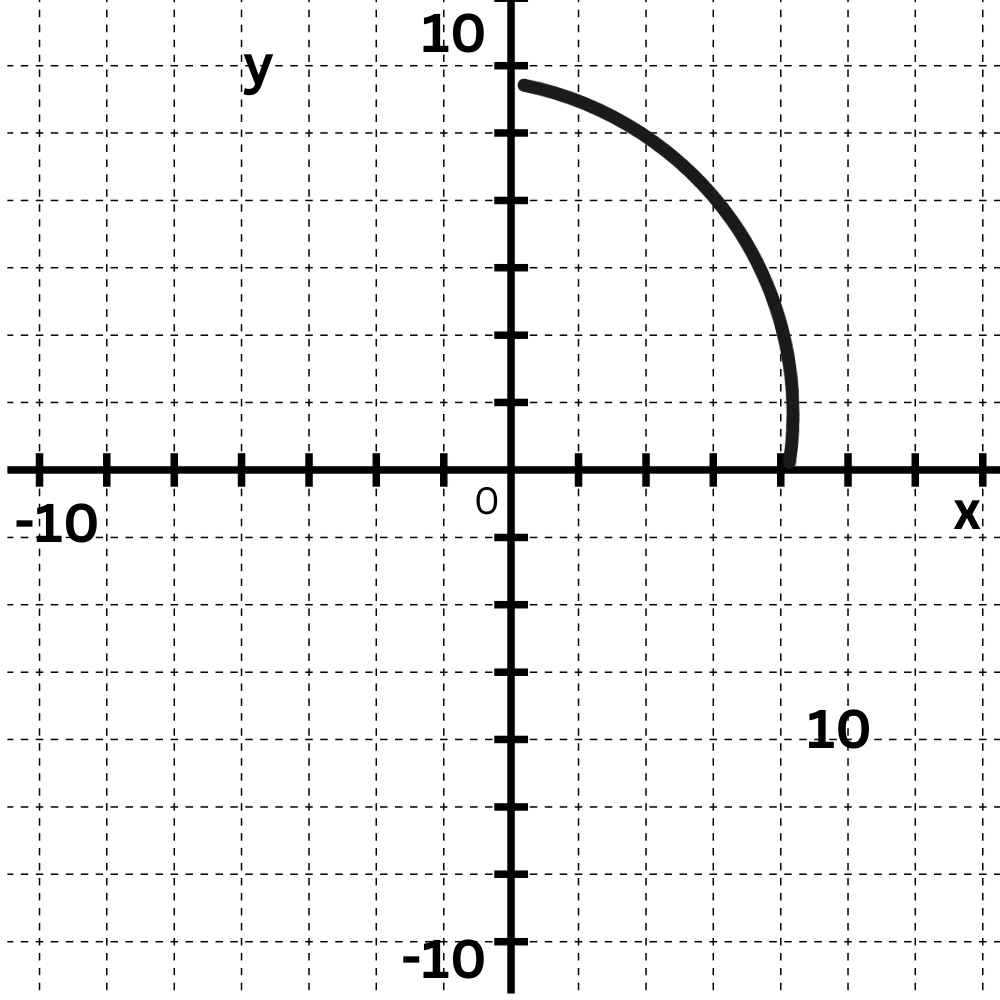
Rotate point T(5, –7) 270° clockwise around the origin. The point will move from Quadrant IV to Quadrant I. To find the exact location, imagine (0, 0) and T forming opposite corners of a box. Rotate the box, keeping the (0, 0) corner fixed. T′ has coordinates (7, 5).
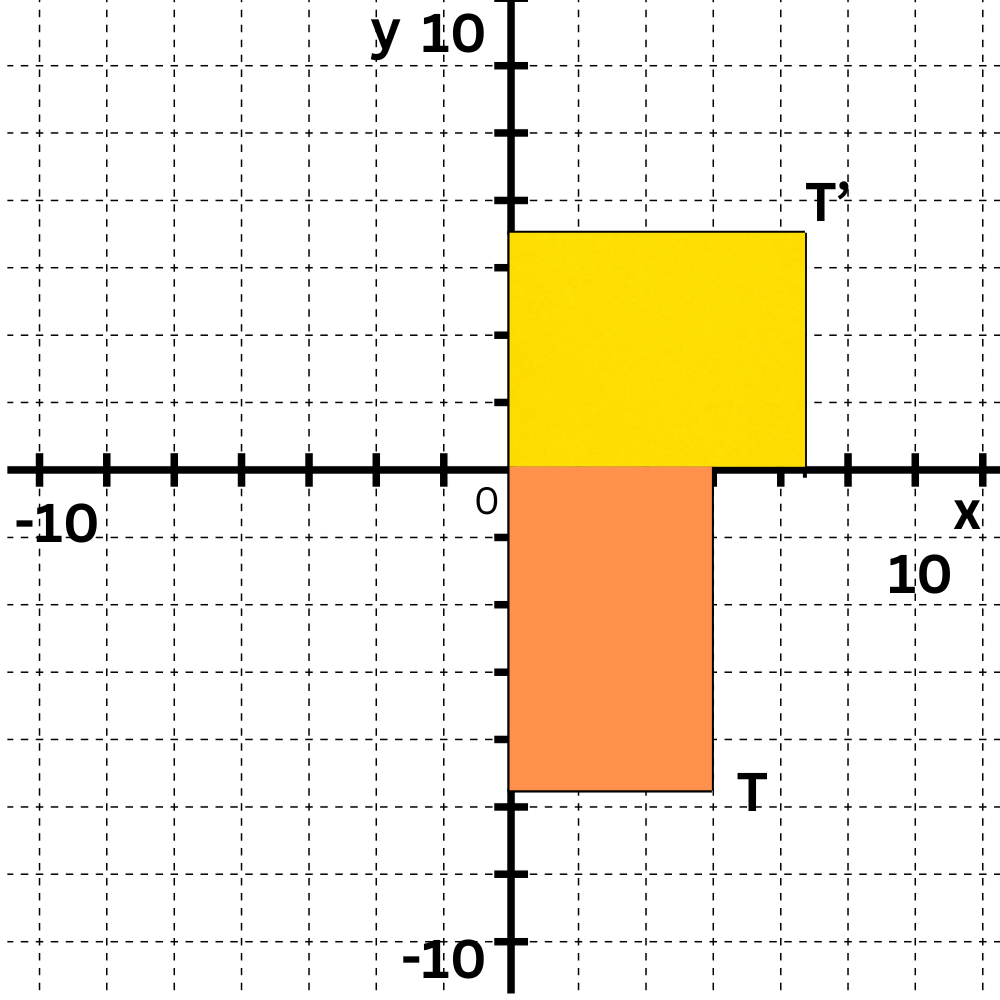
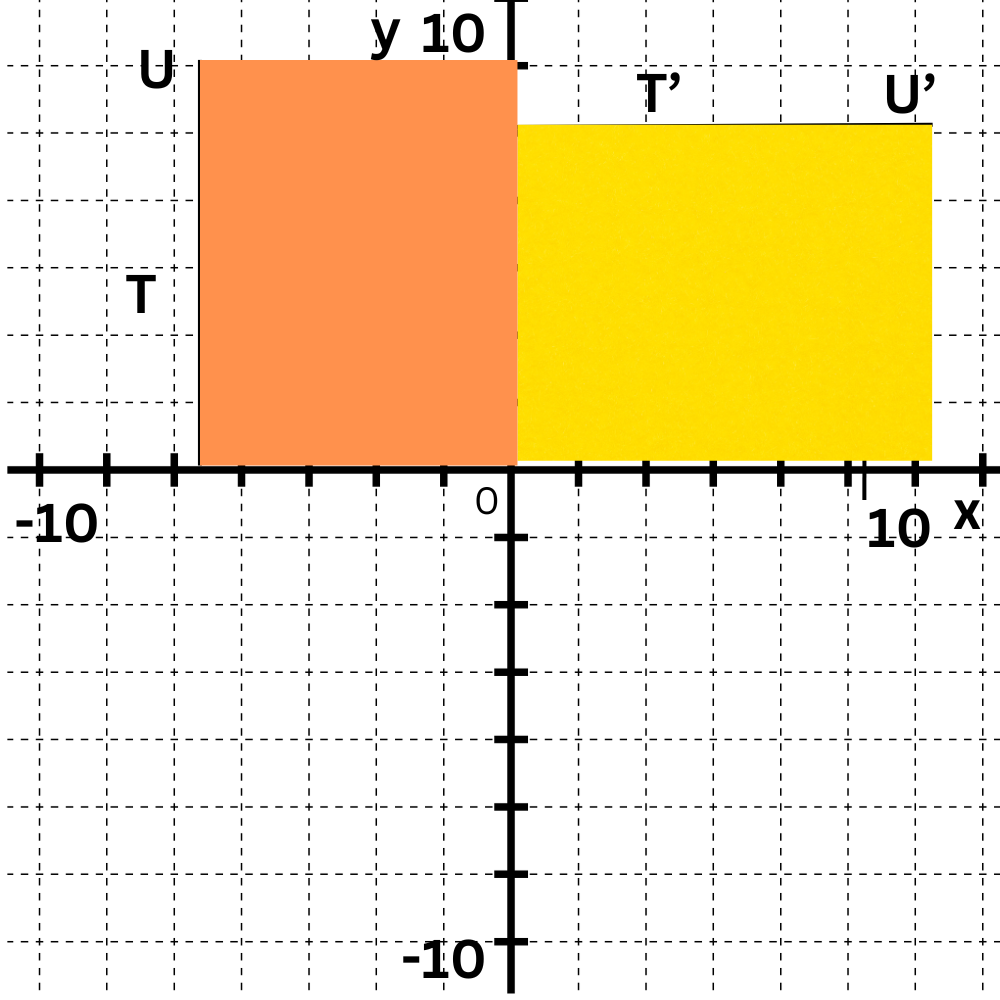
Now rotate point U(5, –6) 270° clockwise around the origin. The point will move from Quadrant IV to Quadrant I. Again, imagine a box to find the exact location. U′ has coordinates (6, 5).
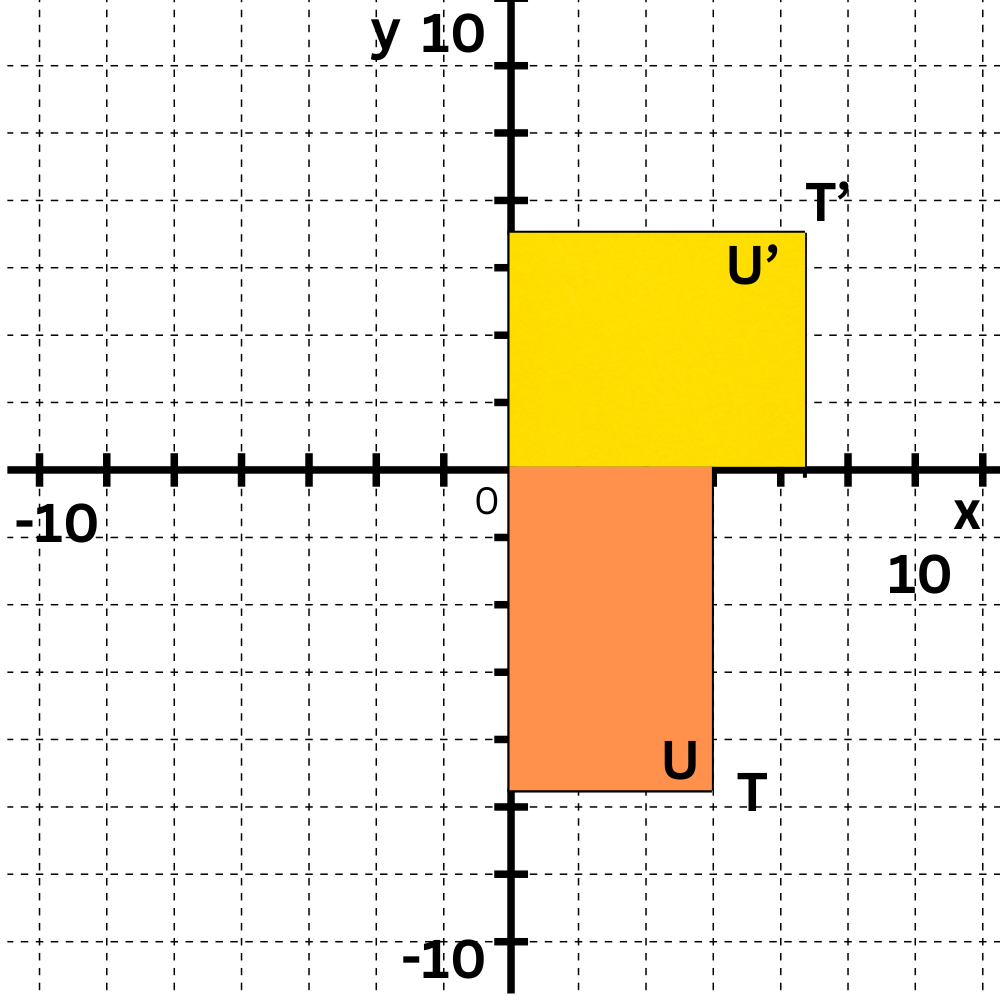
Now rotate points V(7, –6) and W(7, –7) 270° clockwise around the origin. V′ has coordinates (6, 7) and W′ has coordinates (7, 7).
The rotated points form a rectangle congruent to TUVW.
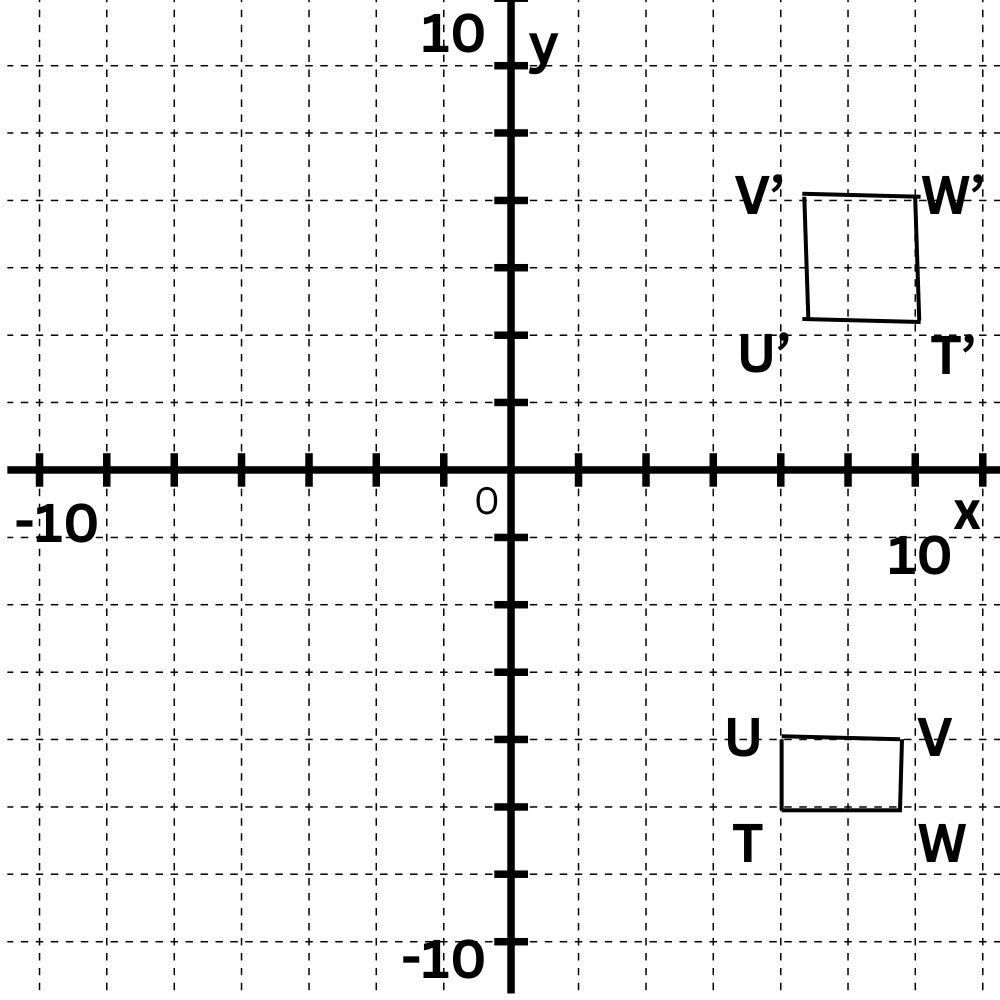
Write the coordinates of the vertices using arrow notation:
T(5 , -7) ——> T'(7 , 5)
U(5 ,-6)——>U'(6 , 5)
V(7 , -6)——>V'(6 , 7)
W(7 , 7)——>W'(7 , 7)
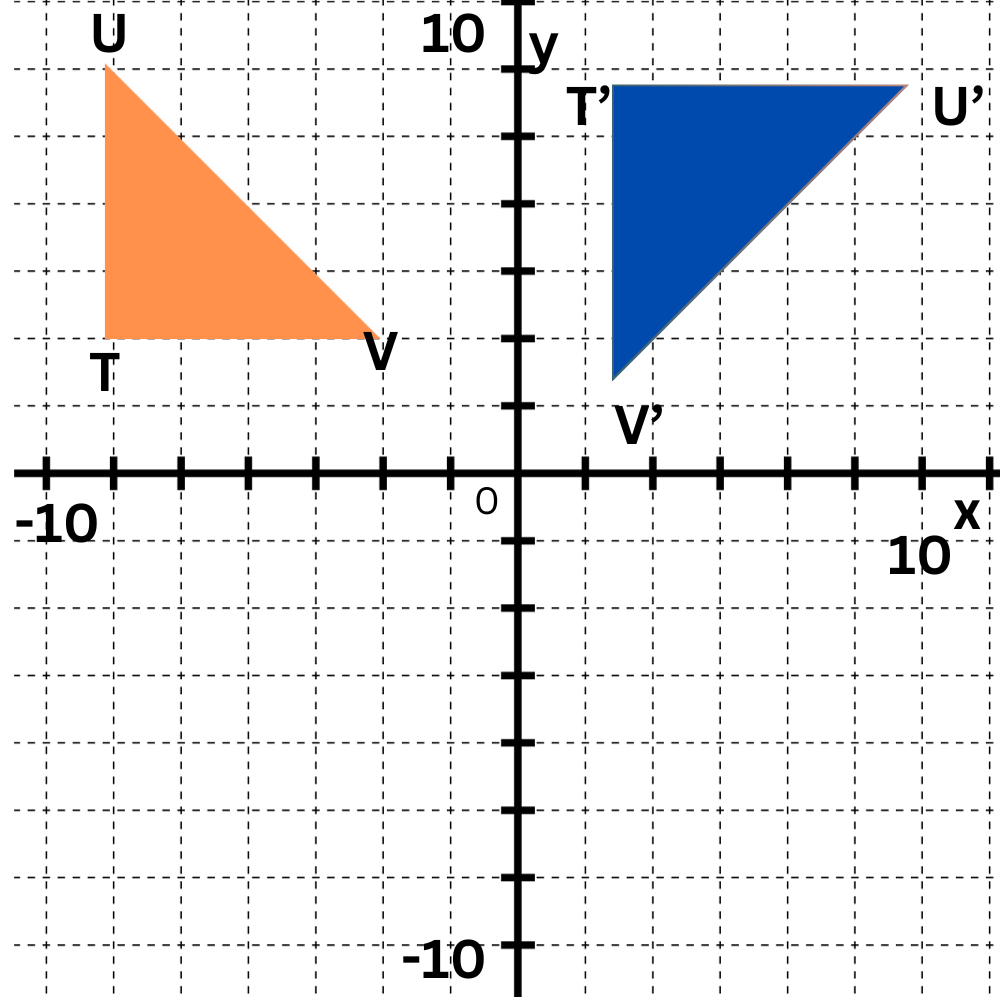
Write the coordinates of the vertices after a rotation 90° clockwise around the origin.
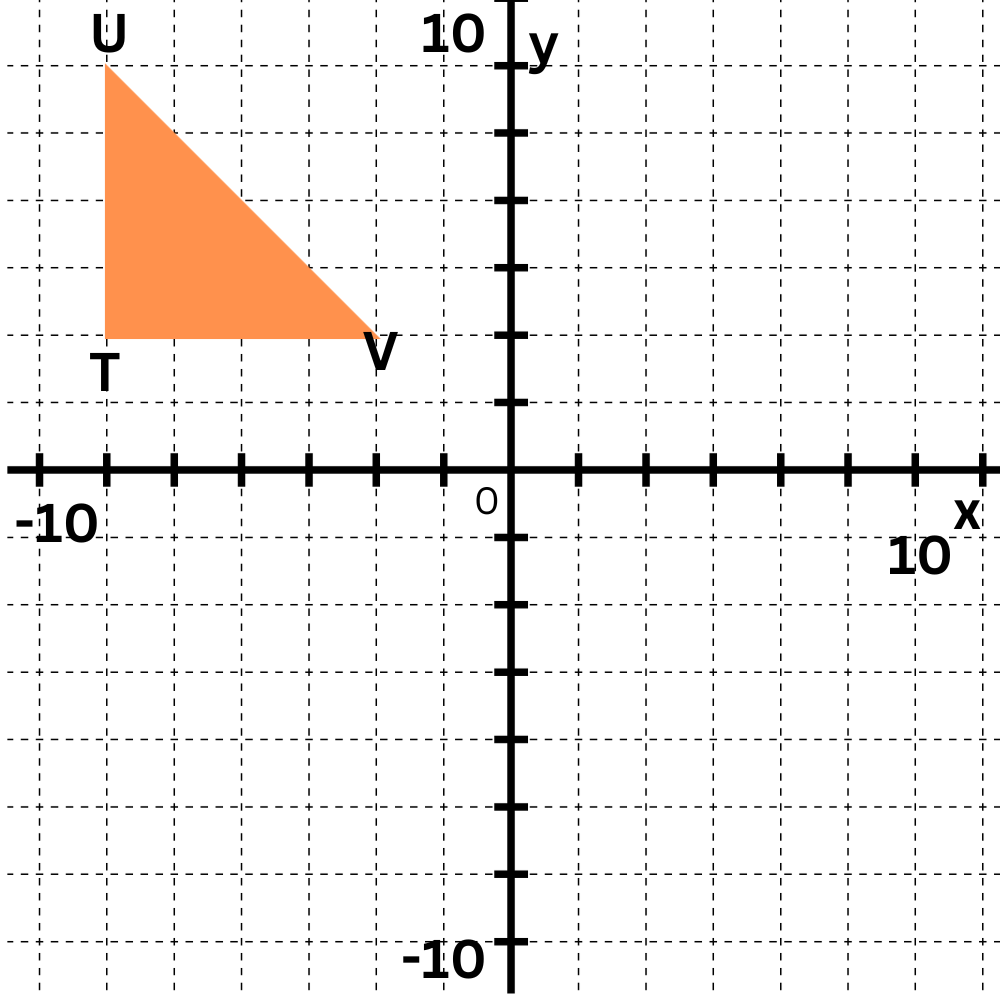
T (-8 , 3)——> T'(____ , ____)
U(-8 ,10)——>U'(____ , ____)
V(-3 , 3)——>V'(____ , ____)
90°is 1/4 of a full turn . The rotation will turn the triangle 1/4 of a full turn in the clockwise direction.
Rotate point T(–8, 3) 90° clockwise around the origin. The point will move from Quadrant II to Quadrant I. To find the exact location, imagine (0, 0) and T forming opposite corners of a box. Rotate the box, keeping the (0, 0) corner fixed. T′ has coordinates (3, 8).
Now rotate point U(–8, 10) 90° clockwise around the origin. The point will move from Quadrant II to Quadrant I. Again, imagine a box to find the exact location. U′ has coordinates (10, 8).
Now rotate point V(–3, 3) 90° clockwise around the origin. V′ has coordinates (3, 3).The rotated points form a triangle congruent to ![]() TUV.
TUV.
Write the coordinates of the vertices using arrow notation:
T (-8 , 3)——> T'(3 , 8)
U(-8 ,10)——>U'(10 , 8)
V(-3 , 3)——>V'(3 , 3)
let’s practice!

