Area and perimeter of similar figures
Key Notes :
The following proportion applies to similar shapes:
( a/b)2 = A1/A2
where a/b is the ratio of the corresponding side lengths, and A1/A2 is the ratio of the areas.
Learn with an example
The figures below are similar. The labelled sides are corresponding.
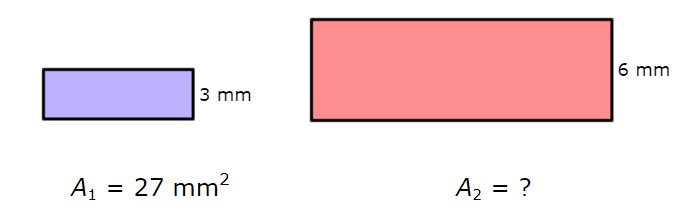
What is the area of the larger rectangle?
A2 = ____________ square millimeters
Find the square of the ratio of the corresponding side lengths.
(a/b)2 = (3/6)2 = (1/2)2 = 1/4
Find the ratio of the areas.
A1 / A2 = 27 / A2
Use these two ratios to set up a proportion and solve for A2.
1/4 = 27/A2
1/4 (4A2) = 27 / A2 (4A2) Multiply both sides by 4A2
A2 = 27 .4 Simplify
A2 = 108 Simplify
The area of the larger rectangle is 108 square millimeters.
The figures below are similar. The labelled sides are corresponding.
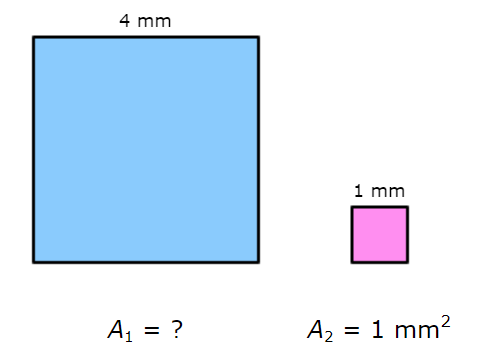
What is the area of the larger square?
A1 = ____________ square millimeters
Find the square of the ratio of the corresponding side lengths.
(a/b)2 = (4/1)2 = 16/1
Find the ratio of the areas.
A1 / A2 = A1 / 1
Use these two ratios to set up a proportion and solve for A1
16/1 = A1/1
16/1 (1 .1) = A1 / 1 (1 .1) Multiply both sides by 1 .1
16 .1 = A1 Simplify
16 = A1 Simplify
The area of the larger rectangle is 16 square millimeters.
The figures below are similar. The labelled sides are corresponding.
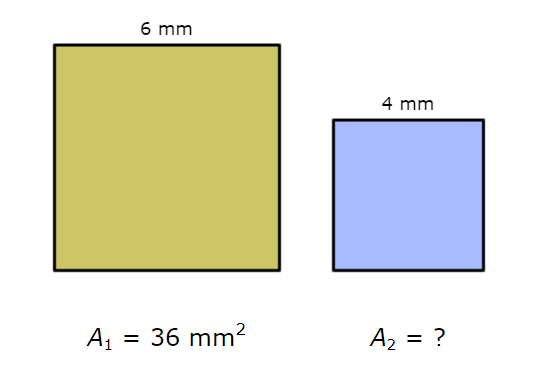
What is the area of the smaller square?
A2 = ____________ square millimeters
Find the square of the ratio of the corresponding side lengths.
(a/b)2 = (6/4)2 = (3/2)2 = 9/4
Find the ratio of the areas.
A1 / A2 = 36 / A2
Use these two ratios to set up a proportion and solve for A2.
9/4 = 36/A2
9/4 (4A2) = 36 / A2 (4A2) Multiply both sides by 4A2
9 A2 = 36 .4 Simplify
9 A2 = 144 Simplify
9 A2 ÷ 9 = 144 ÷ 9 Divide both sides by 9
A2 = 16
The area of the larger rectangle is 16 square millimeters.
Let’s practice!

