Area of compound figures
Key Notes :
- Decomposition: Compound figures are often made up of simpler geometric shapes like rectangles, triangles, circles, etc. Break down the compound figure into these basic shapes to make the problem more manageable.
- Individual Area Calculations: Calculate the area of each component shape separately using the appropriate formula. For example, the area of a rectangle is length multiplied by width, the area of a triangle is (base multiplied by height) divided by 2, and the area of a circle is π times the square of the radius.
- Addition and Subtraction: After finding the areas of individual components, combine them appropriately. If there are overlapping regions, subtract the area of the overlapped region to avoid double counting.
- Units: Always include units in your final answer. The area is measured in square units, so make sure to square the units of length used in the problem.
- Practice with Real-world Scenarios: Relate compound figures to real-world scenarios. This can help in understanding the practical applications of calculating areas of complex shapes, such as determining the total floor space of irregularly shaped rooms.
- Application of Formulas: Reinforce the use of area formulas for different shapes. It’s crucial to know the formulas for squares, rectangles, triangles, circles, and any other shapes that might be encountered in compound figures.
Learn with an example
What is the area of this figure?

Write your answer using decimals. Use 3.14 for 𝜋. square
_______ centimetres
Divide the figure into separate shapes:
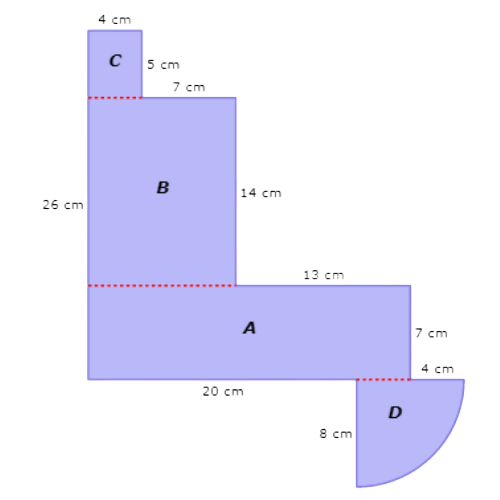
Start with rectangle A. Rectangle A is 24 centimetres wide and 7 centimetres tall.
Multiply:
24 . 7 = 168
The area of rectangle A is 168 cm2.
Look at rectangle C. Rectangle C is 4 centimetres wide and 5 centimetres tall.
Multiply:
4 . 5 = 20
The area of rectangle C is 20 cm2.
Look at quarter circle D. Quarter circle D has a radius of 8 centimetres.
Solve for the area of quarter circle D.
3.14 . 82 / 4 = 50 . 24
The area of quarter circle D is 50.24 cm2.
Now add the areas of all the shapes.
168 cm2 + 154 cm2 + 20 cm2 + 50.24 cm2 = 392.24 cm2
The area is 392.24 square centimetres.
What is the area of this figure?

Write your answer using decimals. Use 3.14 for 𝜋. square
______ millimetres
Divide the figure into separate shapes:
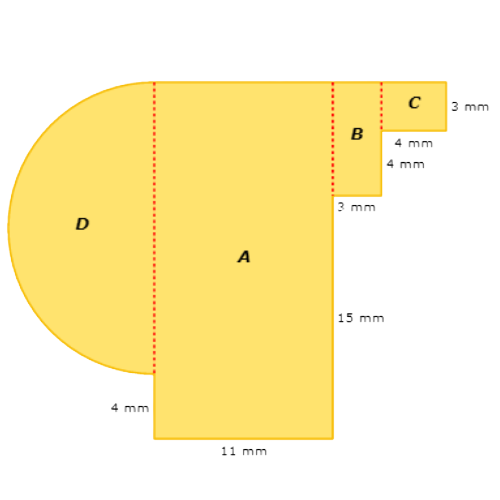
Start with rectangle A. Rectangle A is 11 millimetres wide and 22 millimetres tall.
Multiply:
11 . 22 = 242
The area of rectangle A is 242 mm2.
Look at rectangle B. Rectangle B is 3 millimetres wide and 7 millimetres tall.
Multiply:
3. 7 = 21
The area of rectangle B is 21 mm2.
Look at rectangle C. Rectangle C is 4 millimetres wide and 3 millimetres tall.
Multiply:
4 . 3 = 12
The area of rectangle C is 12 mm2.
Look at semicircle D. Semicircle D has a diameter of 18 millimetres, which gives it a radius of 9 millimetres.
Solve for the area of semicircle D.
3 . 14 . 92 / 2 = = 127.17
The area of semicircle D is 127.17 mm2.
Now add the areas of all the shapes.
242 mm2 + 21 mm2 + 12 mm2 + 127.17 mm2 = 402.17 mm2
The area is 402.17 square millimetres.
What is the area of this figure?

Write your answer using decimals. Use 3.14 for 𝜋.
________ square kilometres
Divide the figure into separate shapes:
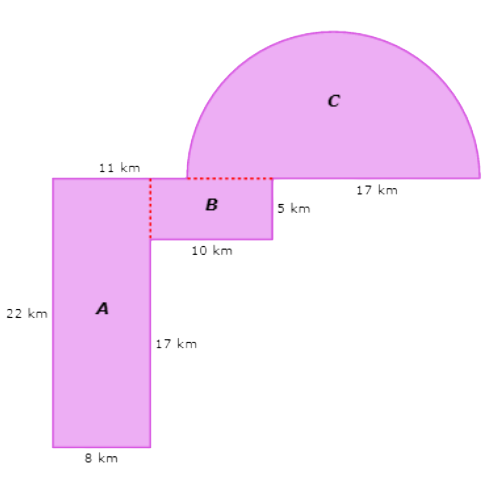
Start with rectangle A. Rectangle A is 8 kilometres wide and 22 kilometres tall.
Multiply:
8 . 22 = 176
The area of rectangle A is 176 km2.
Look at rectangle B. Rectangle B is 10 kilometres wide and 5 kilometres tall.
Multiply:
10 . 5 = 50
The area of rectangle B is 50 km2.
Look at semicircle C. Semicircle C has a diameter of 24 kilometres, which gives it a radius of 12 kilometres.
Solve for the area of semicircle C.
3.14 . 122 / 2 = 226.08
The area of semicircle C is 226.08 km2.
Now add the areas of all the shapes.
176 km2 + 50 km2 + 226.08 km2 = 452.08 km2
The area is 452.08 square kilometres.
let’s practice!🖊️

