Area and perimeter in the coordinate plane II
Key Notes :
Perimeter of a square:
Perimeter = 4s
Area of a square:
Area = s2
Learn with an example
✈️ What is the perimeter of square HIJK?
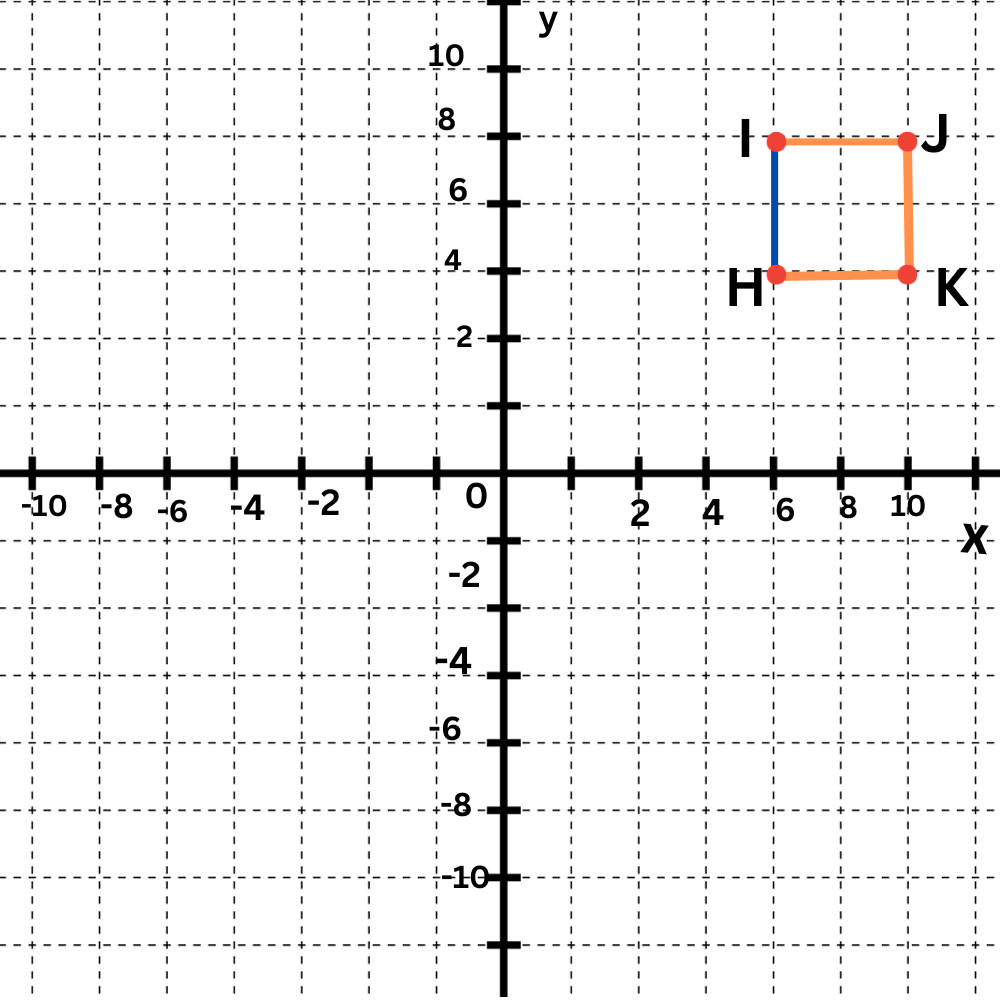
Write your answer as an integer or as a decimal rounded to the nearest tenth.
Perimeter = _____ units
- Look at the graph of square HIJK to find the coordinates of the vertices.
- To find the perimeter of square HIJK, first calculate its side length. Then, plug this value into the formula for the perimeter of a square.
- Step 1: Find the side length.
- All sides of a square have the same length. So, pick any of the four sides.
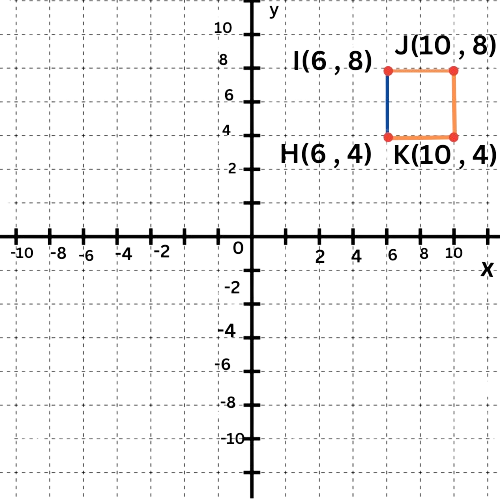
- The distance between the vertices H(6,4) and I(6,8) is the side length of the square.
- Since H(6,4) and I(6,8) have the same x-coordinate, HI is the absolute value of the difference in the y-coordinates, which is |4–8|=4. So, the length is 4.
- Step 2: Find the perimeter.
- Now, plug in the value for the side length into the formula for the perimeter of a square.
- Perimeter of a square
- = 4s
- = 4(4) Plug in s=4
- = 16 Multiply
- So, the perimeter of square HIJK is 16 units.
✈️ What is the perimeter of square BCDE?

Write your answer as an integer or as a decimal rounded to the nearest tenth.
Perimeter = _____ units
Look at the graph of square BCDE to find the coordinates of the vertices.

To find the perimeter of square BCDE, first calculate its side length. Then, plug this value into the formula for the perimeter of a square.
Step 1: Find the side length.
All sides of a square have the same length. So, pick any of the four sides.

The distance between the vertices B(0 , -2) and C(-1 , -2) is the side length of the square .
Since B(0 , -2) and C(-1 , -2) have the same Y- coordinate , BC is the absolute value of the difference in the X- coordinates , which is |0 _ -1| = 1 . So , the length is 1.
Step 2 : Find the perimeter .
Now plug the value for the side length into the formula for the perimeter of a square
Perimeter of a square = 4S
= 4 (1) Plug in s = 1
= 4 Multiply
So the perimeter of square BCDE is 4 Units.
Let’s practice!

