Area and perimeter in the coordinate plane I
Key Notes :
Area of a square:
Area=s2
Learn with an example
✈️ What is the perimeter of square STUV?
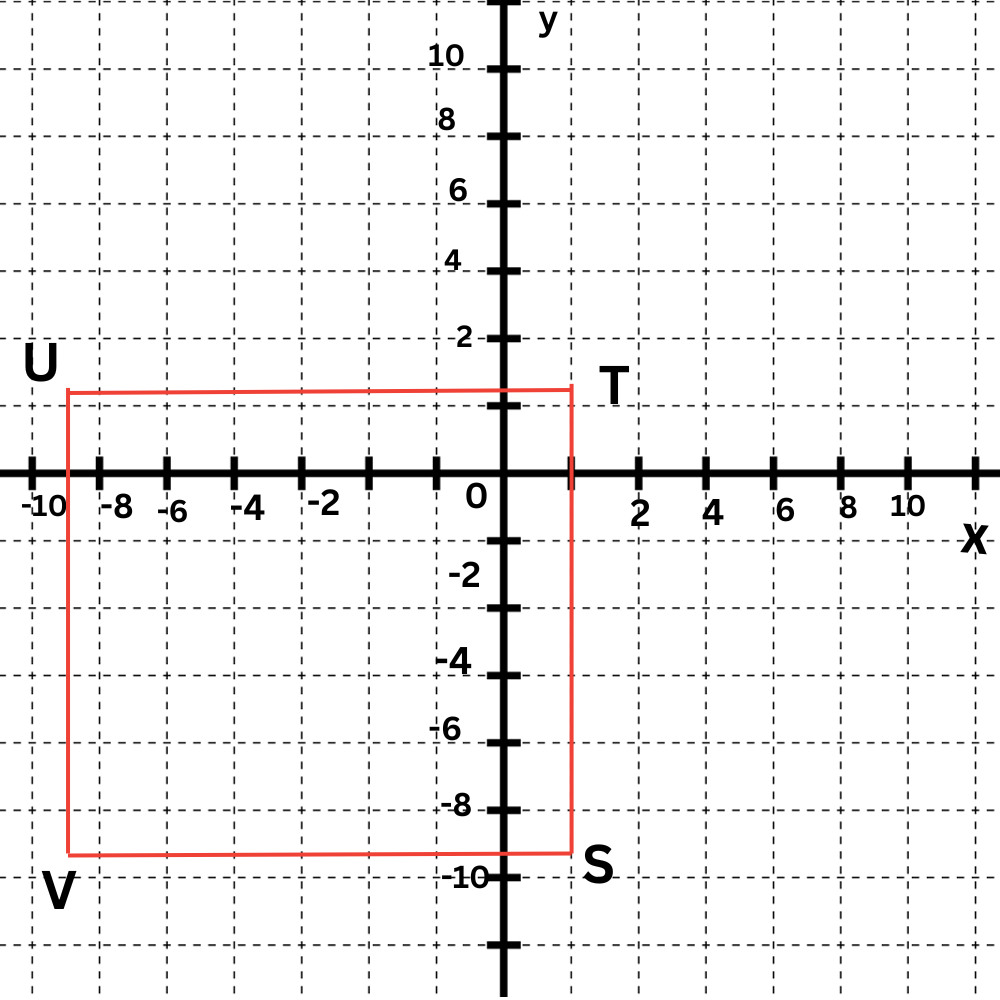
Area= _____ square units
- Look at the graph of square STUV to find the coordinates of the vertices.
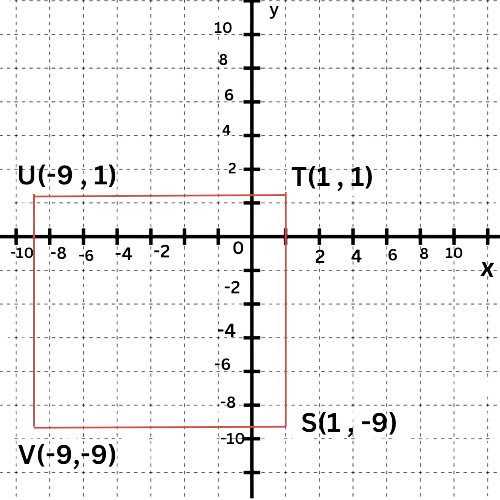
- To find the area of square STUV, first calculate its side length. Then, plug this value into the formula for the area of a square.
- Step 1: Find the side length.
- All sides of a square have the same length. So, pick any of the four sides.
- The distance between the vertices S(1,–9) and T(1,1) is the side length of the square.
- Since S(1,–9) and T(1,1) have the same x-coordinate, ST is the absolute value of the difference in the y-coordinates, which is |–9–1|=10. So, the length is 10.
- Step 2: Find the area.
- Now, plug in the value for the side length into the formula for the area of a square.
- Area of a square
- = s2
- = 102 Plug in s=10
- = 100 Square
- So, the area of square STUV is 100 square units.
✈️ What is the perimeter of square EFGH?
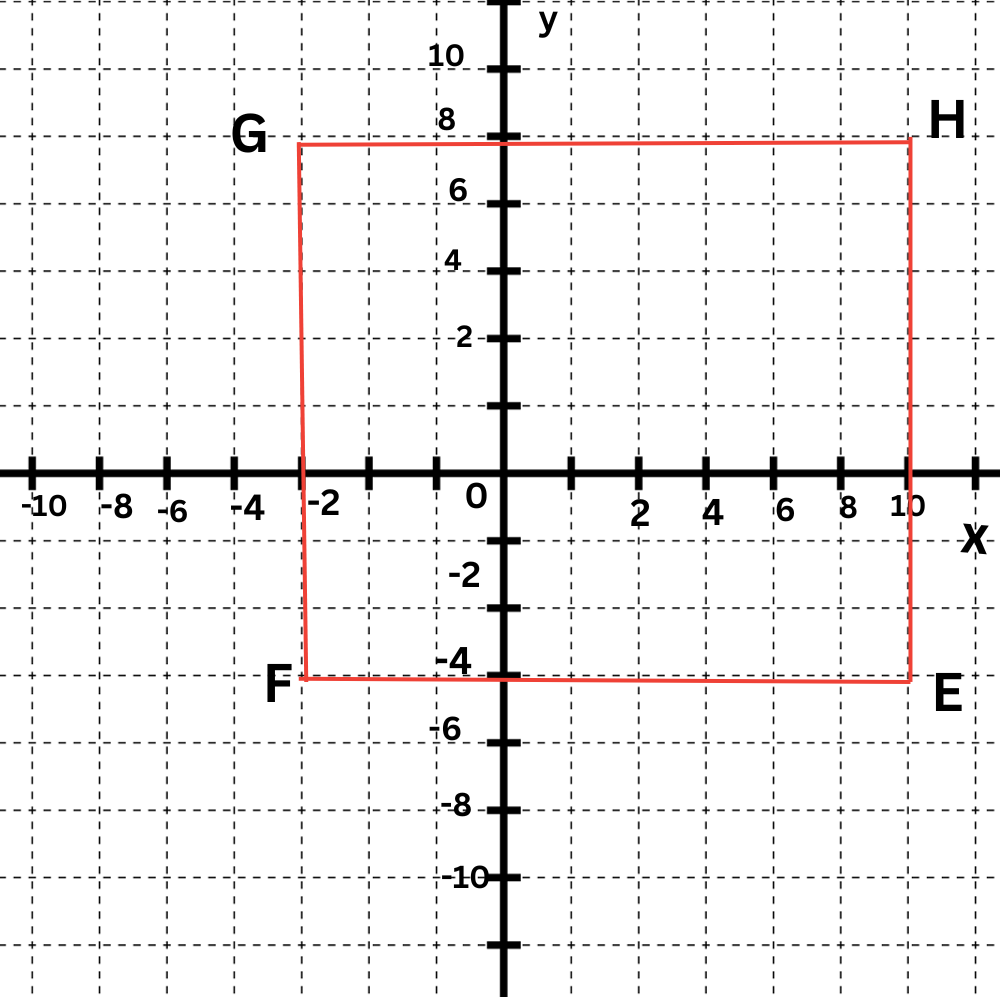
Perimeter= _____ units
- Look at the graph of square EFGH to find the coordinates of the vertices.
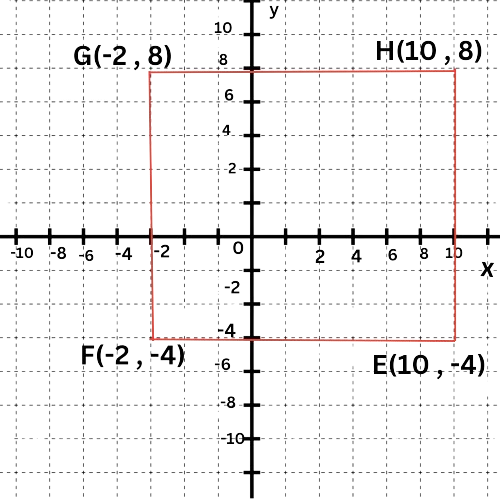
- To find the perimeter of square EFGH, first calculate its side length. Then, plug this value into the formula for the perimeter of a square.
- Step 1: Find the side length.
- All sides of a square have the same length. So, pick any of the four sides.
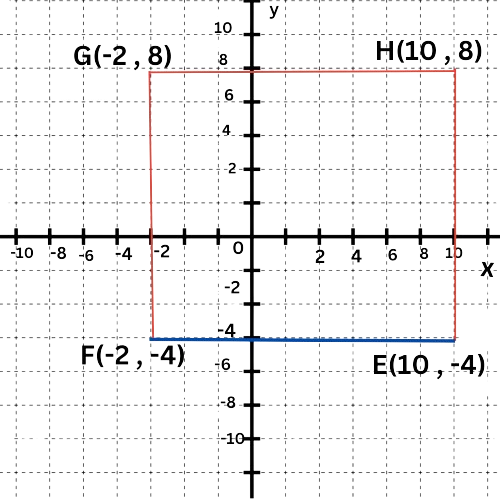
- The distance between the vertices E(10,– 4) and F(–2,–4) is the side length of the square.
- Since E(10,–4) and F(–2,–4) have the same y-coordinate, EF is the absolute value of the difference in the x-coordinates, which is |10– –2|=12. So, the length is 12.
- Step 2: Find the perimeter.
- Now, plug in the value for the side length into the formula for the perimeter of a square.
- Perimeter of a square
- = 4s
- = 4(12) Plug in s=12
- = 48 Multiply
- So, the perimeter of square EFGH is 48 units.
✈️ What is the perimeter of square BCDE?
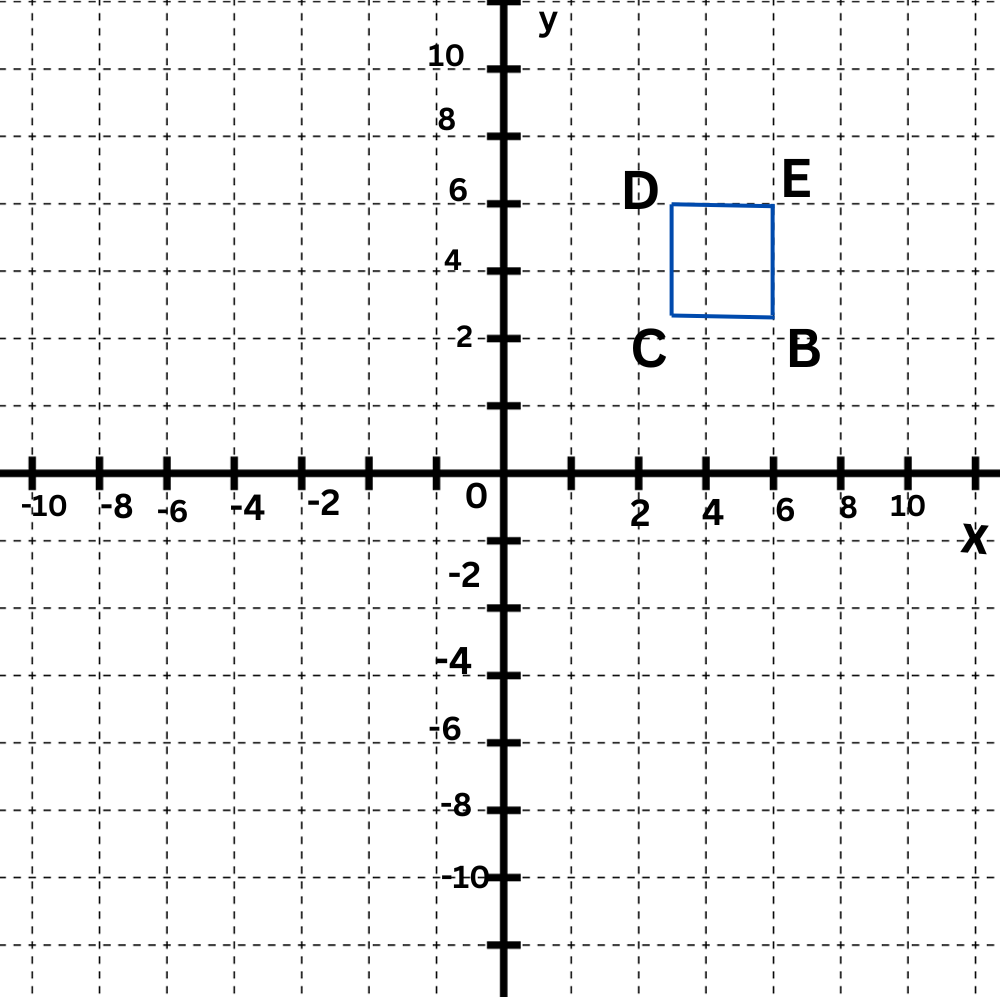
Perimeter= ________ units
- Look at the graph of square BCDE to find the coordinates of the vertices.
- To find the perimeter of square BCDE, first calculate its side length. Then, plug this value into the formula for the perimeter of a square.
- Step 1: Find the side length.
- All sides of a square have the same length. So, pick any of the four sides.
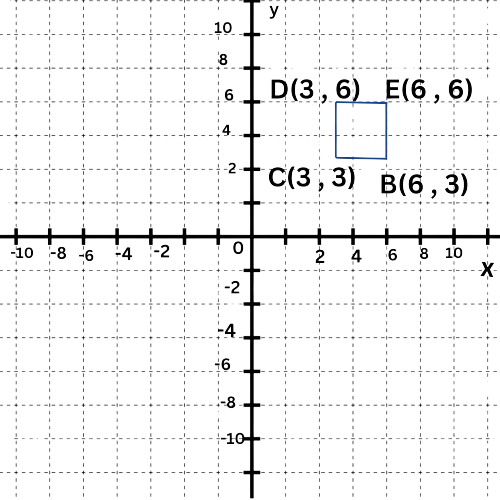
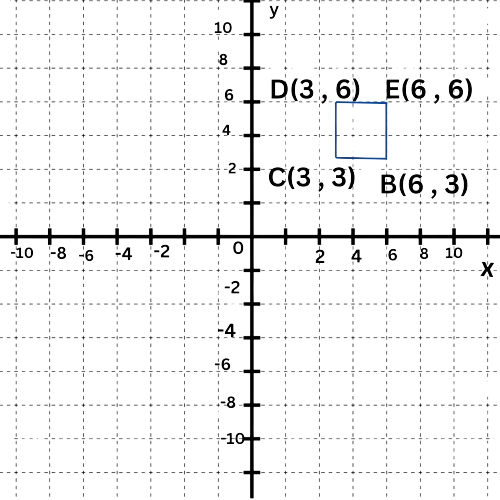
- The distance between the vertices B(6,3) and C(3,3) is the side length of the square.
- Since B(6,3) and C(3,3) have the same y-coordinate, BC is the absolute value of the difference in the x-coordinates, which is |6–3|=3. So, the length is 3.
- Step 2: Find the perimeter.
- Now, plug in the value for the side length into the formula for the perimeter of a square.
- Perimeter of a square
- = 4s
- = 4(3) Plug in s=3
- = 12 Multiply
- So, the perimeter of square BCDE is 12 units.
Let’s practice!

