Midpoint formula
Key Notes :
Midpoint formula :
The Mid point formula is used to find the point that is exactly half way between two given points (x1 , y1 ) and (x2 , y2 ) in a coordinate plane .
Formula :
The mid point (M) between two points (x1 , y1 ) and (x2 , y2 ) is given by :
M = (x1 +x2 /2 , y1 +y2 /2)
Learn with an example
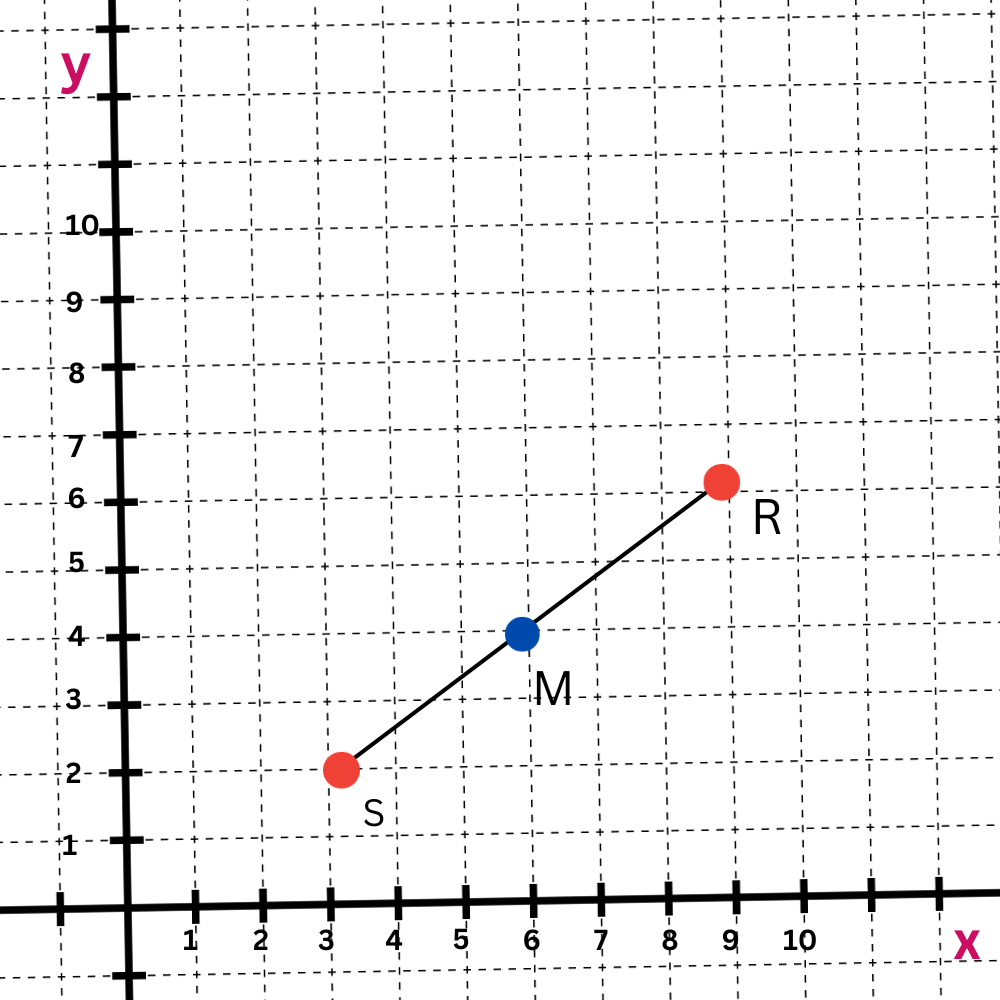
A line segment has the endpoints R(9, 6) and S(3, 2). Find the coordinates of its midpoint M.
Write the coordinates as decimals or integers.
M = ( ____ ______)
Use the mid point formula to find the midpoint M. Plug in R(9 , 6) for (x1 , y1 ) and S(3,2) for (x2 , y2 )
M = (x1 +x2 /2 , y1 +y2 /2)
= (9 + 3/2, 6 + 2/2) Plug in (9,6) and (3,2)
= (12/2, 8/2) Add
= (6, 4) Simplify
RS has its midpoint M at (6, 4)
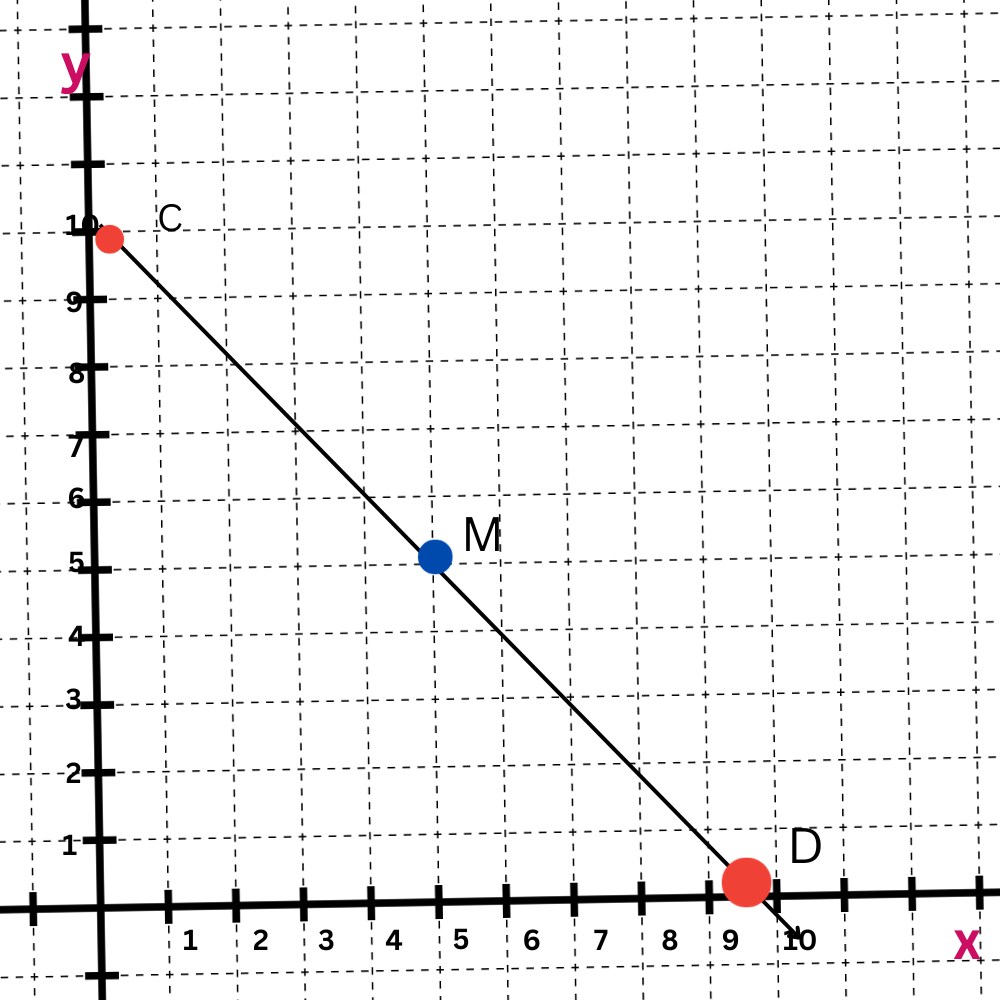
A line segment has the endpoints C(0,10) and D(10, 0). Find the coordinates of its midpoint M.
Write the coordinates as decimals or integers.
M = ( ____ ______)
Use the mid point formula to find the midpoint M. Plug in C(0 , 10) for (x1 , y1 ) and D(10 ,0) for (x2 , y2 )
M = (x1 +x2 /2 , y1 +y2 /2)
=(0 + 10/2, 10 + 0/2) Plug in (0,10) and (10,0)
= (10/2, 10/2) Add
= (5, 5) Simplify
CD has its midpoint M at (5, 5).
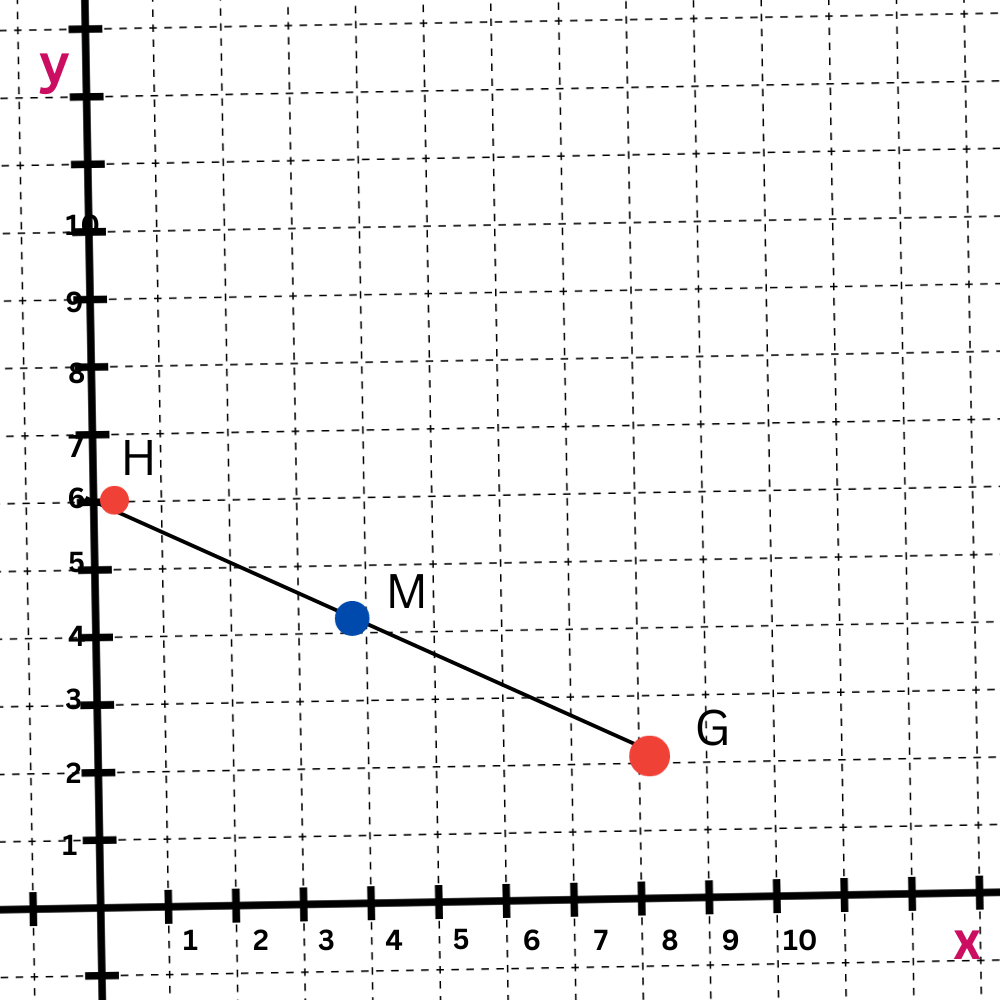
GH has endpoints at G(8, 2) and H(0, 6). Find the midpoint M of GH.
Write the coordinates as decimals or integers.
M = ( ____ ______)
Use the mid point formula to find the midpoint M. Plug in G(8 , 2) for (x1 , y1 ) and H(0 ,6) for (x2 , y2 )
M = (x1 +x2 /2 , y1 +y2 /2)
= (8 + 0/2, 2 + 6/2) Plug in (8,2) and (0,6)
= (8/2, 8/2) Add
= (4, 4) Simplify
GH has its midpoint M at (4, 4).
let’s practice!

