Perpendicular Bisector Theorem
Key Notes :
A point is equidistant from other points if it is the same distance from them.
The Perpendicular Bisector Theorem states that a point is on the perpendicular bisector of a segment if and only if it is equidistant from the endpoints of the segment.
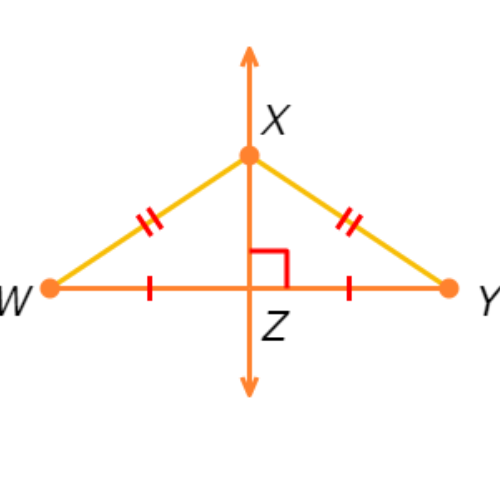
X is on the perpendicular bisector of WY if and only if WX ≅ XY .
Definition:
The Perpendicular Bisector Theorem is a geometric principle that relates to a line segment and its perpendicular bisector.
Statement:
If a point lies on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment.
Key Concepts:
- Perpendicular Bisector:
- A line, segment, or ray that intersects another line segment at its midpoint and forms a right angle (90 degrees) with the segment.
- Equidistant:
- The distance from a point to each endpoint of a segment is equal.
Theorem Statement:
If a point P lies on the perpendicular bisector of segment AB, then PA=PB, where PA and PB are the distances from point P to the endpoints A and B respectively.
Example:
Consider line segment AB with midpoint M. If P is a point on the perpendicular bisector of AB, then PM=PA=PB.
Learn with an example
What is GI?
GI= ______________
Look at the diagram.
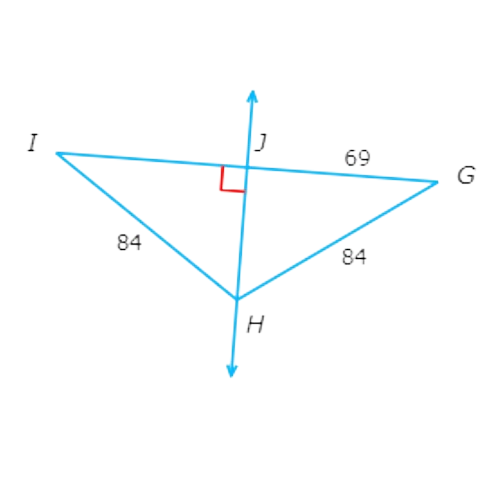
since GH = HI = 84 , H is equidistant from the endpoints of GI . Therefore H lies on the perpendicular bisector of GI by the Perpendicular Bisector Theorem.
Since H is on the perpendicular bisector of GI and HJI is a right angle ,HJ is the perpendicular bisector of GI .
So, GJ = IJ = 69 and G . I = 2.69 = 138.
What is QR?
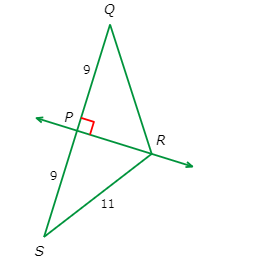
QR=_____________
Look at the diagram.
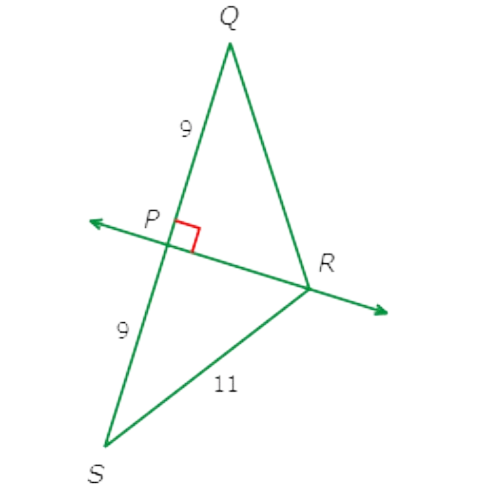
Since ∠QPR is a right angle and PQ = PS = 9 , PR is the perpendicular bisector of QS .
Therefore , QR ≅ RS by the Perpendicular Bisector Theorem.
So , QR = RS = 11.
If QR=RS=66 and ST=42, what is QS?
QS=__________
Label the diagram with the information given in the question.
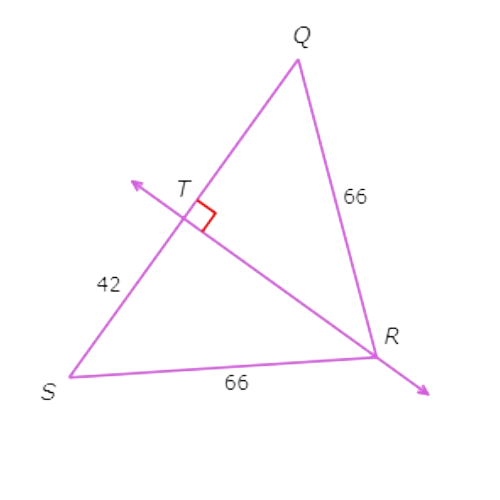
Since QR = RS = 66 , R is equidistant from the endpoints of QS . Therefore R lies on the perpendicular bisector of QS by the Perpendicular Bisector Theorem.
Since R is on the perpendicular bisector of QS and ∠QTR is a right angle ,RT is the perpendicular bisector of QS .
So, QT = ST = 42 and QS = 2. 42 = 84.
let’s practice!

