Congruent line segments
Key Notes :
Two segments are congruent (≅) if they have the same length.
Introduction:
- Definition of Congruence: In geometry, the term “congruence” indicates that two geometric figures are identical in shape and size. When it comes to line segments, congruence implies that two segments have the same length.
- Congruent Line Segments: Line segments are congruent if they have equal lengths. This concept is fundamental in geometry and plays a crucial role in various geometric proofs and constructions.
Properties of Congruent Line Segments:
- Equal Lengths:
- The most fundamental property of congruent line segments is that they have the same length.
- If AB and CD are congruent line segments, then the measure of AB is equal to the measure of CD.
- Symbolic Representation:
- Congruent line segments are often denoted using the symbol ≅.
- For example, if AB≅CD, it signifies that line segments AB and CD are congruent.
Methods of Proving Congruent Line Segments:
- Measurement:
- Direct measurement using a ruler is the simplest way to show that two line segments are congruent.
- Congruence Postulates:
- Side-Side-Side (SSS) Congruence Postulate: If three sides of one triangle are congruent to three sides of another triangle, the triangles are congruent.
- Side-Angle-Side (SAS) Congruence Postulate: If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, the triangles are congruent.
Learn with an example
Are WX and UY congruent?
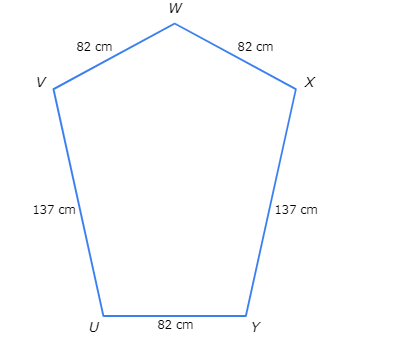
- yes
- no
Look at the diagram and compare WX to UY .
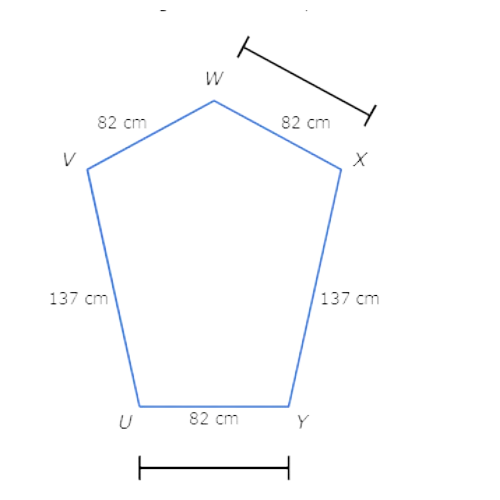
WX is 82 Centimeters long and UY is 82 Centimeters long . WX and UY have the same length , so WX and UY are congruent .
Are EF and FG congruent?
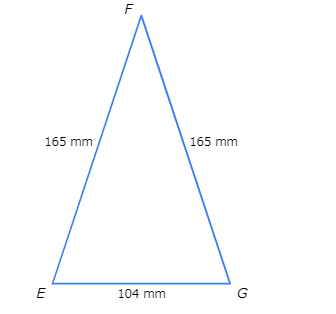
- yes
- no
Look at the diagram and compare EF to FG .
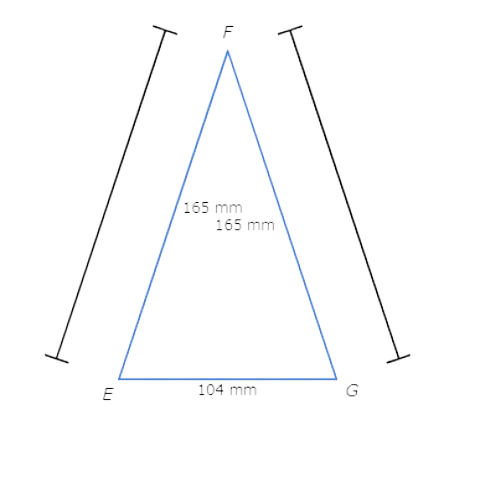
EF is 165 millimeters long and FG is 165 millimeters long . EF and FG have the same same length , so EF and FG are congruent
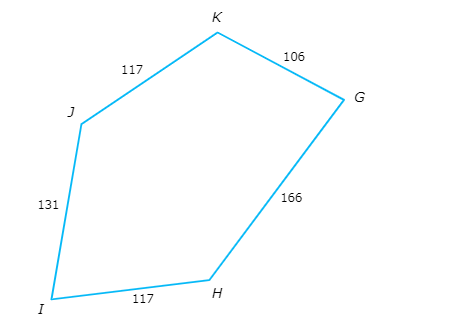
Are IJ and GH congruent?
- yes
- no
Look at the diagram and compare IJ to GH .
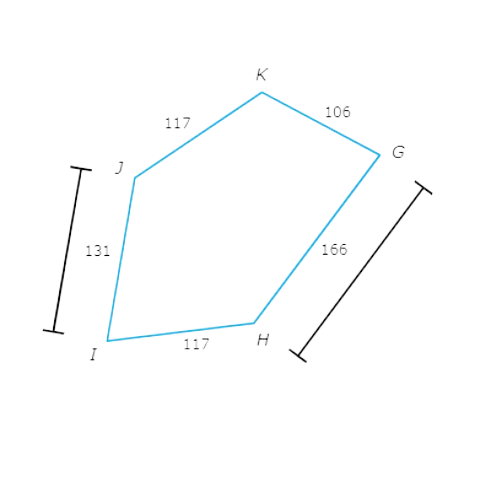
IJ = 131 and GH = 166 . IJ ≠ GH , so IJ and GH are not congruent .
let’s practice!

