Characteristics of quadratic equations
Key Notes :
Quadratic Equations
A quadratic equation is a polynomial equation of degree two. It can be expressed in the general form:
ax² + bx + c = 0
where a, b, and c are constants, and a ≠ 0.
Key Characteristics:
- Degree: The highest power of the variable (x) in a quadratic equation is 2.
- Roots: A quadratic equation has at most two solutions, also known as roots. These roots represent the values of x that make the equation true.
- Nature of Roots:
- Real and Distinct: If the discriminant (b² – 4ac) is positive, the roots are real and distinct.
- Real and Equal: If the discriminant is zero, the roots are real and equal.
- Imaginary or Complex: If the discriminant is negative, the roots are imaginary or complex.
- Sum and Product of Roots:
- Sum of Roots: The sum of the roots of a quadratic equation is -b/a.
- Product of Roots: The product of the roots of a quadratic equation is c/a.
- Graph: The graph of a quadratic equation is a parabola.
- Shape: The shape of the parabola depends on the sign of the coefficient a.
- If a > 0, the parabola opens upward.
- If a < 0, the parabola opens downward.
- Vertex: The vertex of the parabola is the point where the equation changes direction.
- Shape: The shape of the parabola depends on the sign of the coefficient a.
- Completing the Square: This is a technique used to solve quadratic equations by rewriting them in the form (x + h)² = k.
- Quadratic Formula: The quadratic formula is a general formula used to solve quadratic equations:
- x = [-b ± √(b² – 4ac)] / 2a
Additional Points to Consider:
- Factoring: In some cases, quadratic equations can be solved by factoring.
- Discriminant: The discriminant (b² – 4ac) provides information about the nature of the roots.
- Graphing: Understanding the graph of a quadratic equation can help visualize the solutions.
- Applications: Quadratic equations have many applications in various fields, including physics, engineering, and economics.
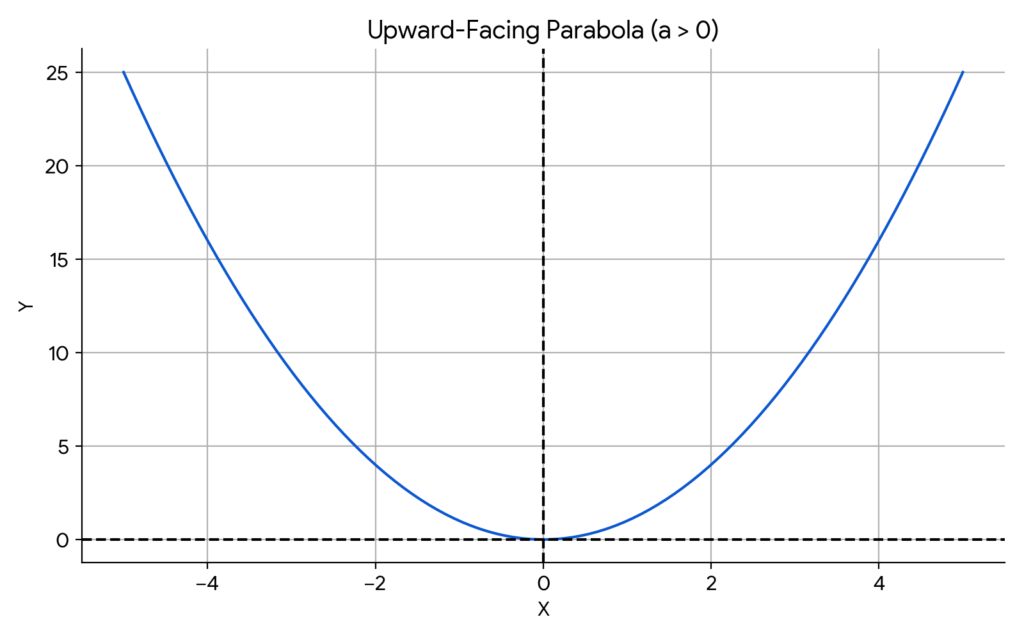
Upward-Facing Parabola
A parabola opens upward when the leading coefficient (a) is positive. This means that the quadratic term, ax², has a positive sign.
Key characteristics of an upward-facing parabola:
- Vertex: The lowest point on the parabola, also known as the minimum point.
- Axis of symmetry: A vertical line that divides the parabola into two symmetrical halves.
- X-intercepts: The points where the parabola intersects the x-axis.
- Y-intercept: The point where the parabola intersects the y-axis.
Example equation:
- y = x²
In this equation, the leading coefficient is 1, which is positive, resulting in an upward-facing parabola.
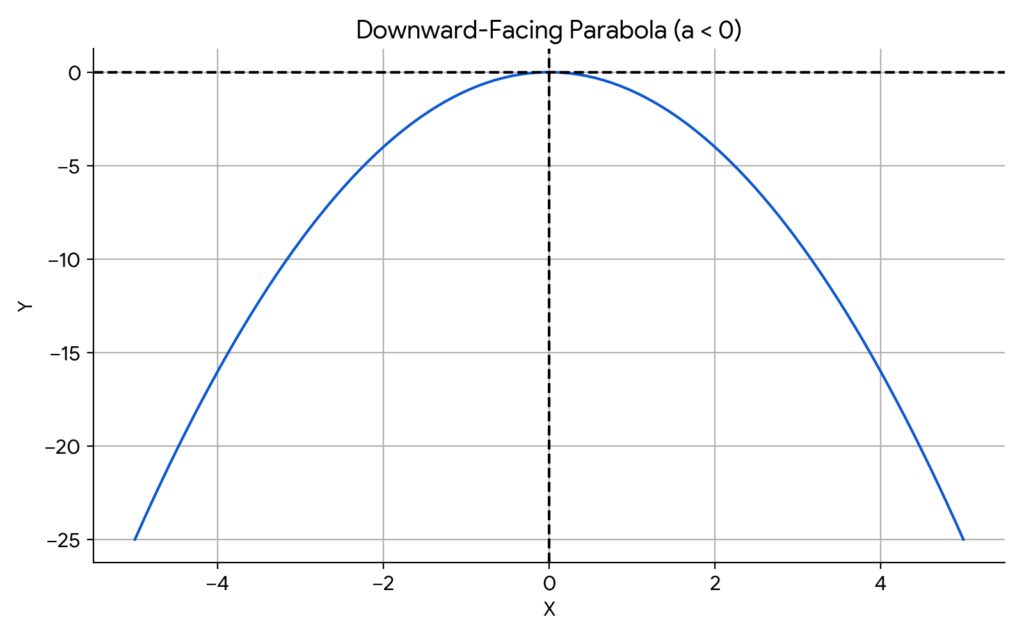
Downward-Facing Parabola
A parabola opens downward when the leading coefficient (a) is negative. This means that the quadratic term, ax², has a negative sign.
Key characteristics of a downward-facing parabola:
- Vertex: The highest point on the parabola, also known as the maximum point.
- Axis of symmetry: A vertical line that divides the parabola into two symmetrical halves.
- X-intercepts: The points where the parabola intersects the x-axis.
- Y-intercept: The point where the parabola intersects the y-axis.
Example equation:
- y = -x²
In this equation, the leading coefficient is -1, which is negative, resulting in a downward-facing parabola.
Learn with an example
Look at this graph:
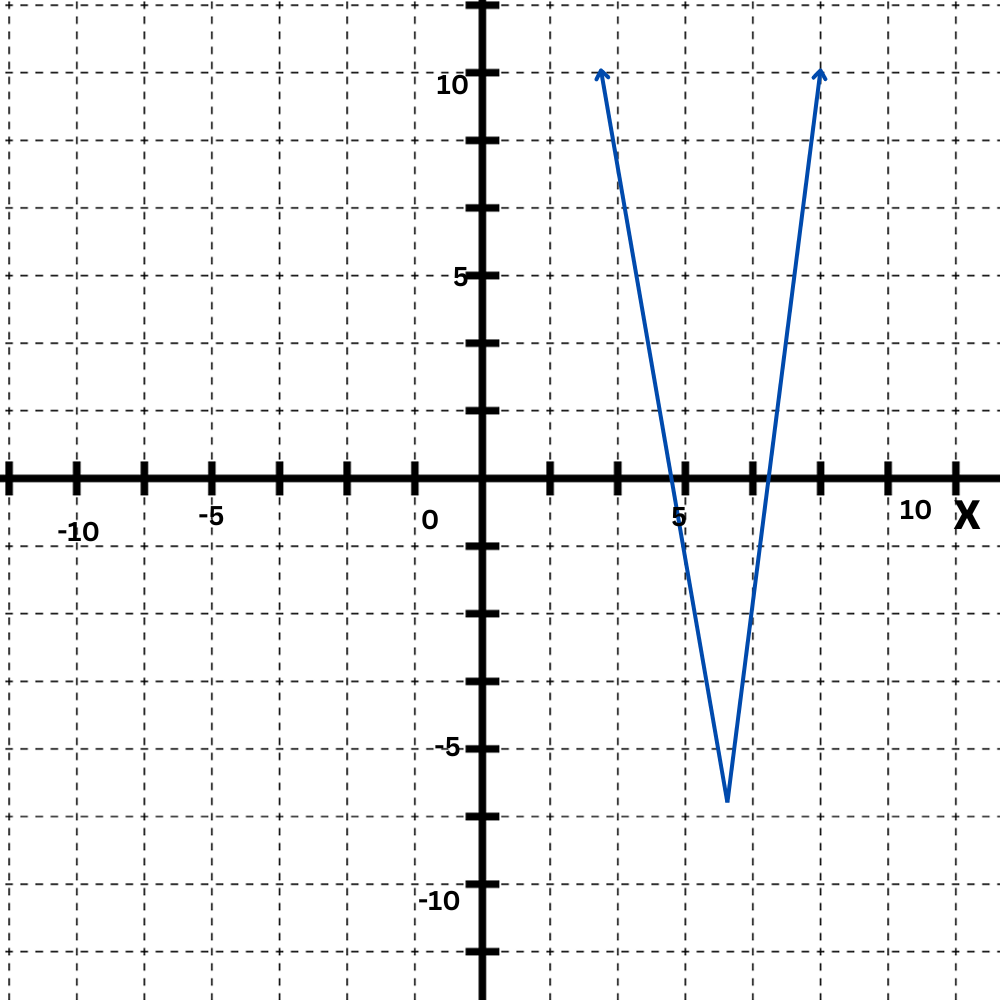
What are the coordinates of the vertex ?
The lowest point on the graph is at(4, –7).

So, the vertex is(4, –7).
Look at this graph:
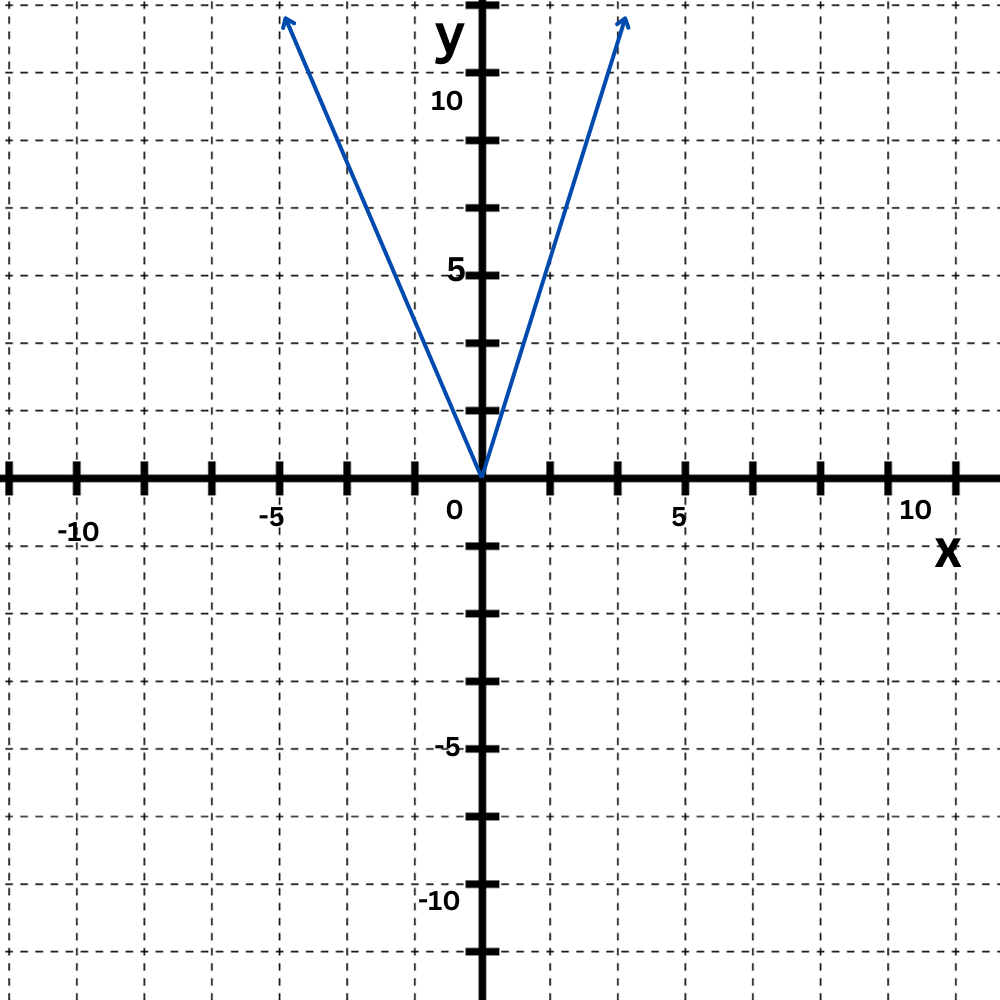
What are the coordinates of the vertex ?
The lowest point on the graph is at(0, 0).
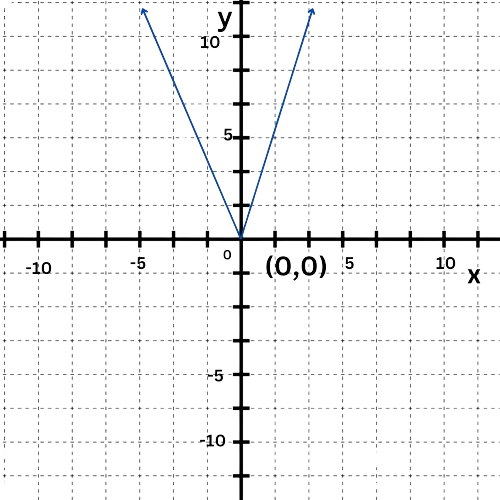
So,the vertex is(0, 0).
Look at this graph:
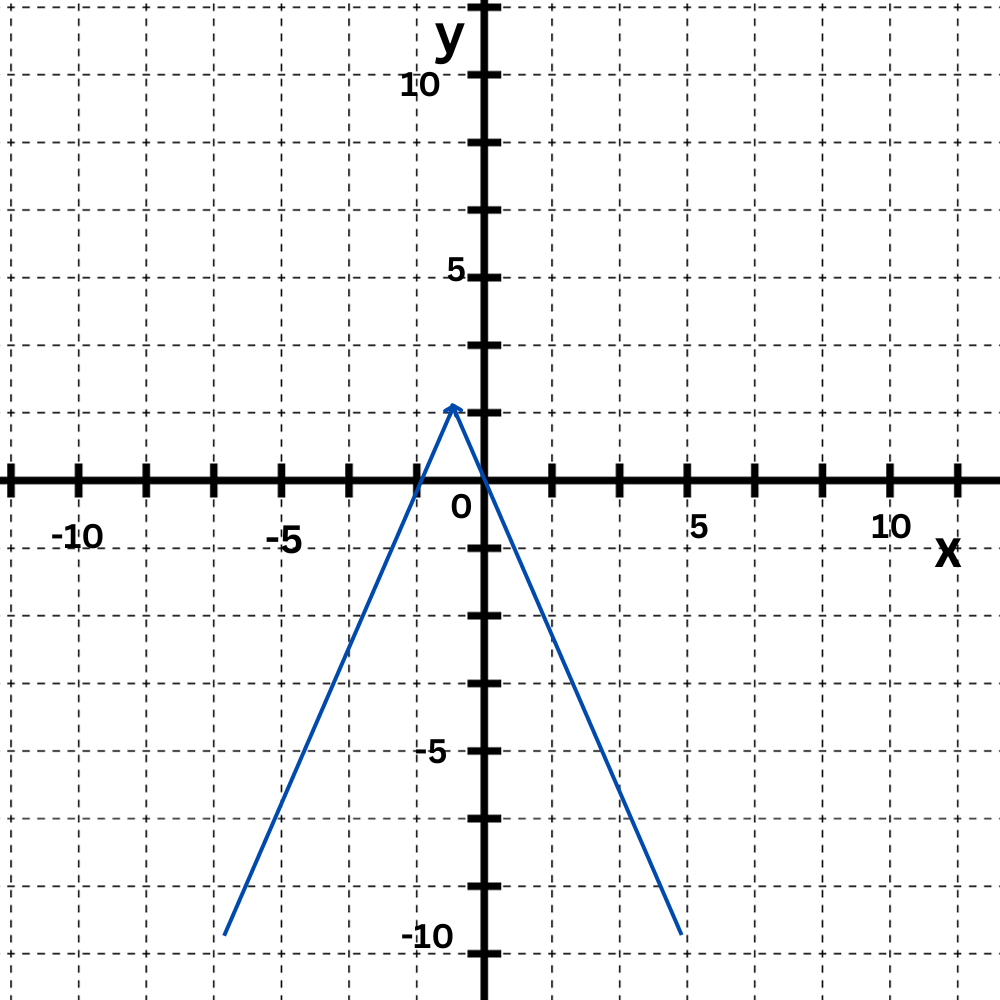
What is the y-intercept ?
The parabola intersects the y-axis at 0.
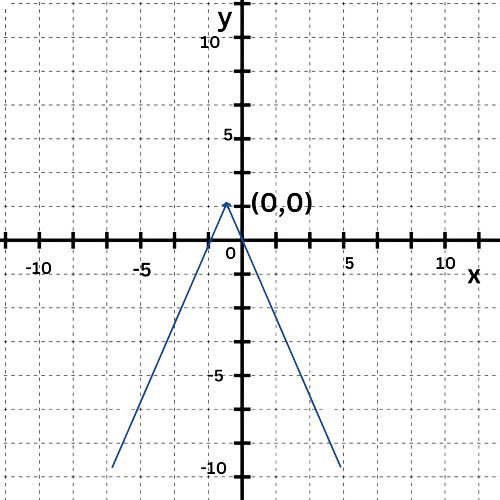
So,the y-intercept is 0.
Let’s practice!

