Factorise polynomials
key notes:
Factorizing perfect square trinomials:
a2+2ab+b2=(a+b)2
a2–2ab+b2=(a–b)2
To factorize a quadratic of the form x2+bx+c, write it as
(x+r1)(x+r2)
where c=r1 . r2 and b=r1+r2.
If a polynomial has four terms, you may be able to factor by grouping. Once the terms are in standard order, factor out the highest common factor (HCF) of the first two terms and the HCF of the second two terms. If the expressions in brackets match, you can factor by grouping:
ac+ad+bc+bd
a(c+d)+b(c+d)
(a+b)(c+d)
Learn with an example
Factorise.
k2+10k+25=———
Notice that k2+10k+25 is a perfect square trinomial because it can be written in the form a2+2ab+b2, where a is k and b is 5.
a2+2ab+b2
k2+2k . 5+52
k2+10k+25
Now use the formula for factorizing perfect square trinomials.
a2+2ab+b2=(a+b)2
k2+2k . 5+52=(k+5)2
k2+10k+25=(k+5)2
The factorized form of k2+10k+25 is (k+5)2.
Finally, check your work.
(k+5)2
(k+5)(k+5)Expand
k2+5k+5k+25 Apply the distributive property (FOIL)
k2+10k+25
Yes, k2+10k+25=(k+5)2.
Factorise.
f2–4f+3=————————
Look at the given quadratic:
f2–4f+3
The c term is 3, so you need to find a pair of factors with a product of 3. The b term is –4, so you need to find a pair of factors with a sum of –4. Since the product is positive (3) and the sum is negative (–4), you need both factors to be negative.
Make a list of the possible factor pairs with a product of 3, and then find the one with a sum of –4.
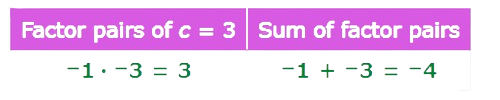
The factors –1 and –3 have a sum of –4. Use those numbers to factorize f2–4f+3.
f2–4f+3
(f–1)(f–3)
Finally, check your work.
(f–1)(f–3)
f2–f–3f+3 Apply the distributive property (FOIL)
f2–4f+3
Yes, f2–4f+3=(f–1)(f–3).
Factor.
7tu–14t+3u–6=——–
Factor by grouping.
7tu–14t+3u–6
7t(u–2)+3(u–2) Factor by grouping; the expressions in brackets should match
(7t+3)(u–2) Apply the distributive property
let’s practice!

