Factorise quadratics using algebra tiles
key notes:
- Introduction to Quadratic Equations:
- Quadratic equations are second-degree polynomial equations in the form ax² + bx + c = 0.
- They can be solved using various methods, and one approach is factorization.
- Understanding Algebra Tiles:
- Algebra tiles are physical or virtual manipulatives used to visualize algebraic expressions and equations.
- In the context of factorizing quadratics, we use algebra tiles to represent the quadratic expression in a visual way.
- Representation of Quadratics with Algebra Tiles:
- Square tiles represent the area model for the quadratic expression.
- Rectangle tiles represent the linear term.
- Unit tiles represent the constant term.
- Factorization Process:
- Arrange the tiles to form a rectangle (representing the quadratic expression).
- Look for ways to break down the rectangle into two smaller rectangles, each representing a linear expression.
- The side lengths of the rectangles will correspond to the factors of the quadratic expression.
- Example: Factorizing x² + 5x + 6:
- Represent x² + 5x + 6 using algebra tiles.
- Arrange the tiles to form a rectangle.
- Find dimensions that allow you to factor the quadratic expression.
- Write the factored form as (x + m)(x + n), where m and n are the dimensions.
- Special Cases: Perfect Square Trinomials:
- If the quadratic expression is a perfect square trinomial, it can be factored into the square of a binomial.
- Example: �2+6�+9x2+6x+9 can be factored as (�+3)2(x+3)2.
- Practice and Application:
- Practice using algebra tiles for various quadratic expressions.
- Apply the factoring technique to solve quadratic equations.
- Verify solutions by multiplying the factors.
- General Formulas for Quadratic Factorization:
- Factorizing ��2+��+�ax2+bx+c involves finding two numbers whose product is ac and whose sum is b.
- The factored form is then (��+�)(��+�)(mx+p)(nx+q), where m, n, p, and q are the constants.
- Review and Homework:
- Review the process of factorization using algebra tiles.
- Assign homework exercises to reinforce the concept.
Learn with an example
Which area model represents the factorization
3x2+12x+9=(x+3)(3x+3)?

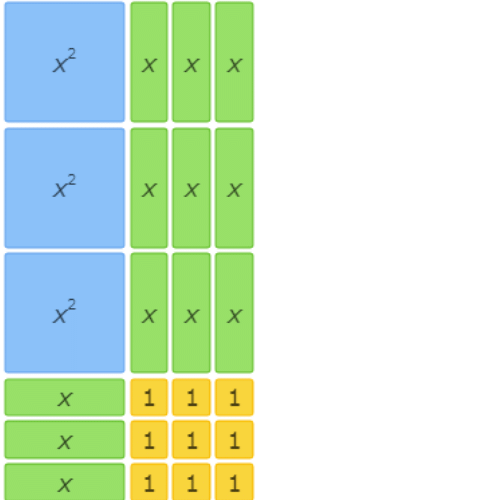
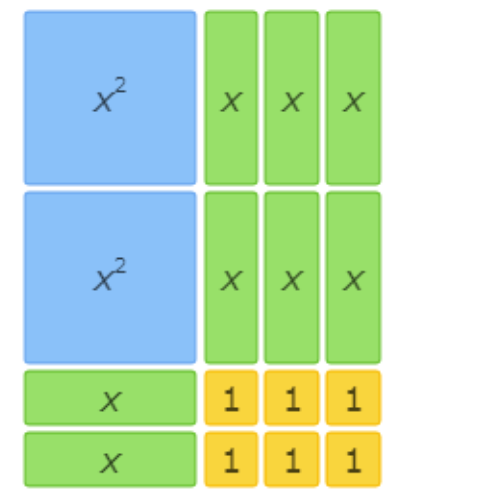
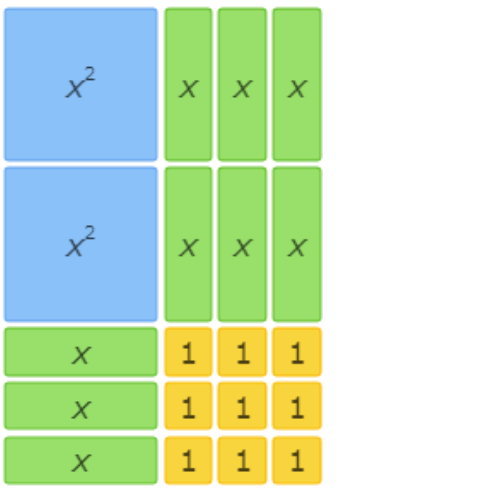
This area model represents the factorization 3x2+12x+9=(x+3)(3x+3).
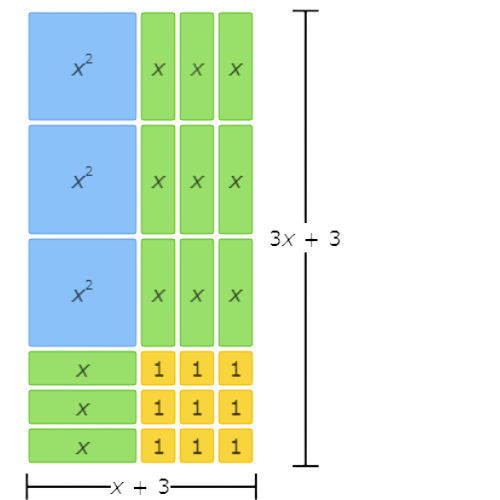
The left side of the equation represents the total area written as the sum of all the tiles. There are 3 x2 tiles, 12 x tiles, and 9 1 tiles, so the sum is 3x2+12x+9.
The right side of the equation represents the total area written as base times height. The base is made up of 1 x tile and 3 1 tiles, so it is (x+3). The height is made up of 3 x tiles and 3 1 tiles, so it is (3x+3). The base times the height is (x+3)(3x+3).
The other area models represent factorizations of different polynomials.
This area model shows 3x2+11x+6=(x+3)(3x+2).
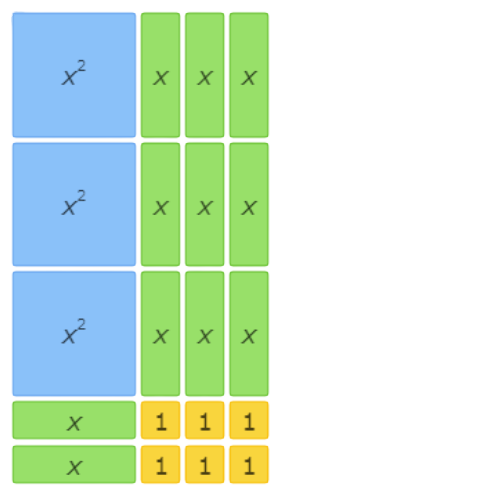
This area model shows 2x2+8x+6=(x+3)(2x+2).
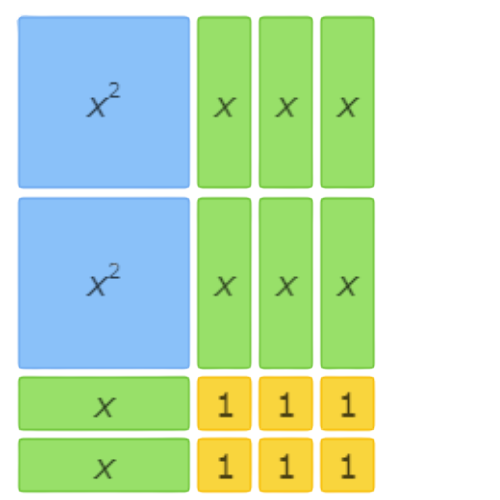
This area model shows 2x2+9x+9=(x+3)(2x+3).
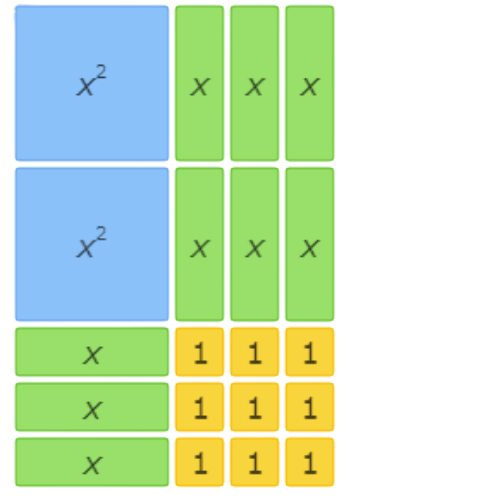
Which area model represents the factorization
6x2+13x+6=(2x+3)(3x+2)?
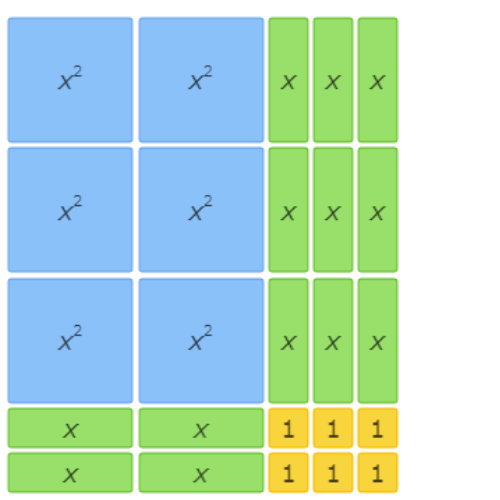
This area model represents the factorization 6x2+13x+6=(2x+3)(3x+2).
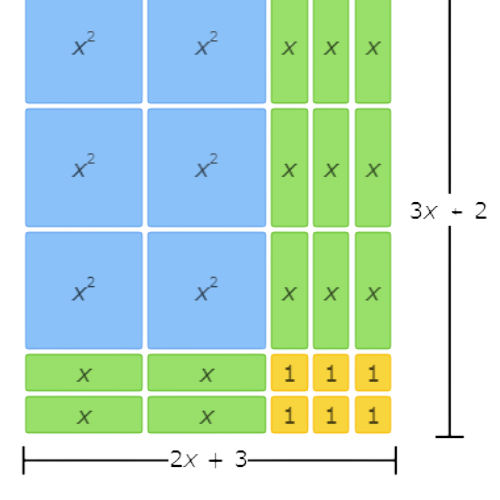
The left side of the equation represents the total area written as the sum of all the tiles. There are 6 x2 tiles, 13 x tiles, and 6 1 tiles, so the sum is 6x2+13x+6.
The right side of the equation represents the total area written as base times height. The base is made up of 2 x tiles and 3 1 tiles, so it is (2x+3). The height is made up of 3 x tiles and 2 1 tiles, so it is (3x+2). The base times the height is (2x+3)(3x+2).
The other area models represent factorizations of different polynomials.
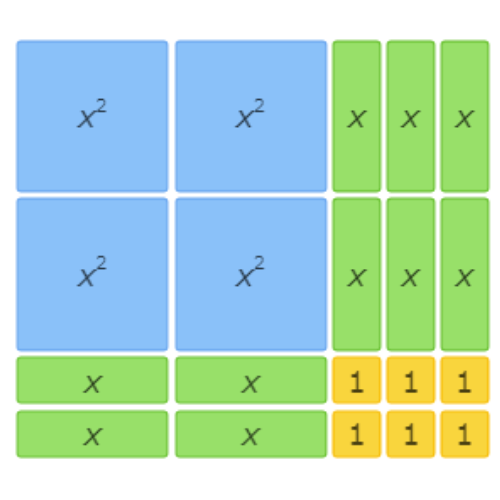
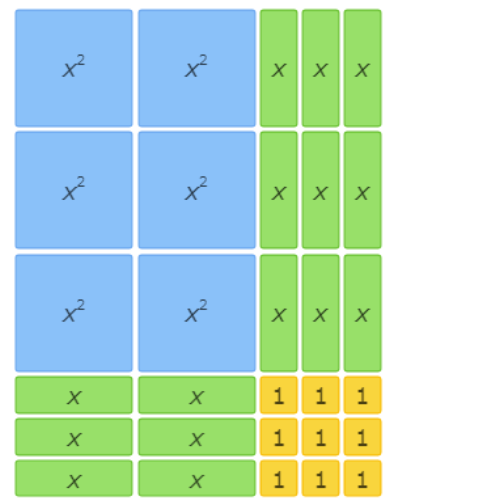
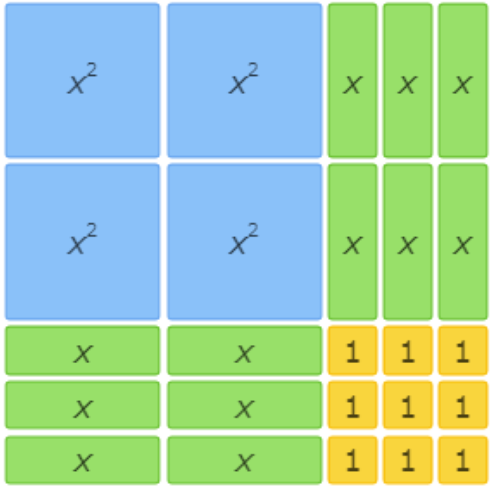
This area model shows 4x2+10x+6=(2x+3)(2x+2).
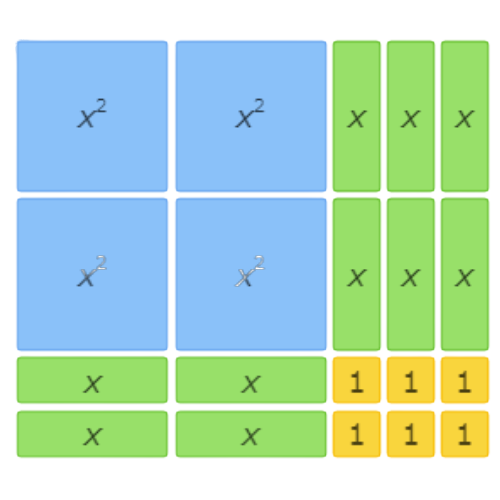
This area model shows 6x2+15x+9=(2x+3)(3x+3).
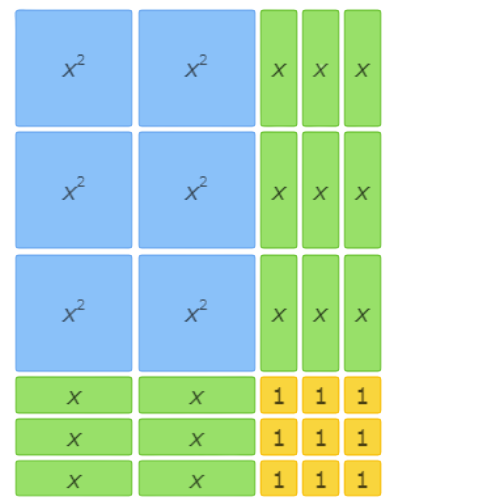
This area model shows 4x2+12x+9=(2x+3)(2x+3).
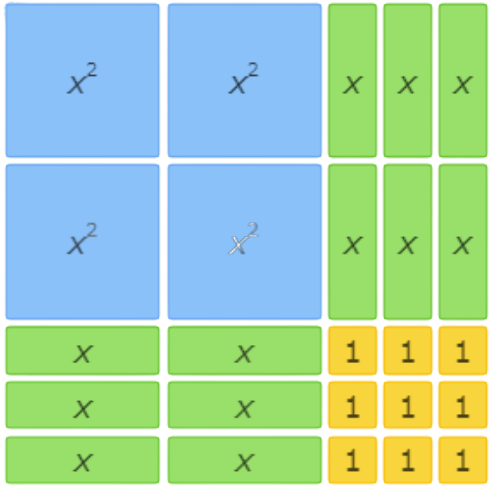
Which area model represents the factorization
3x2+6x+3=(3x+3)(x+1)?
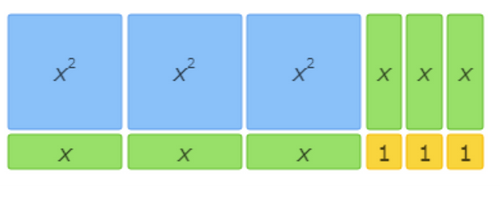
This area model represents the factorization 3x2+6x+3=(3x+3)(x+1).
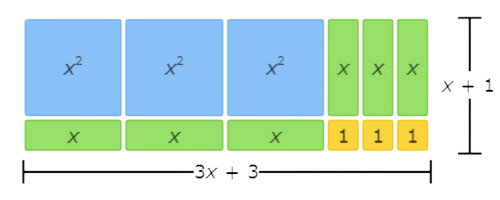
The left side of the equation represents the total area written as the sum of all the tiles. There are 3 x 2 tiles, 6 x tiles, and 3 1 tiles, so the sum is 3x2+6x+3.
The right side of the equation represents the total area written as base times height. The base comprises 3 x tiles and 3 1 tiles, so it is (3x+3). The height is 1 x tile and 1 1 tile, so it is (x+1). The base times the height is (3x+3)(x+1).
The other area models represent factorizations of different polynomials.
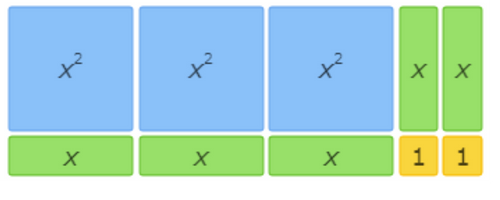
This area model shows 3x2+5x+2=(3x+2)(x+1).
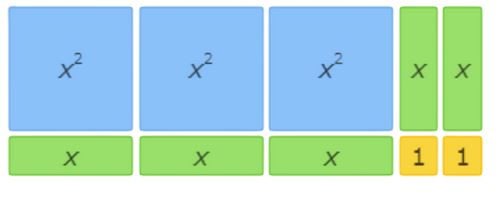
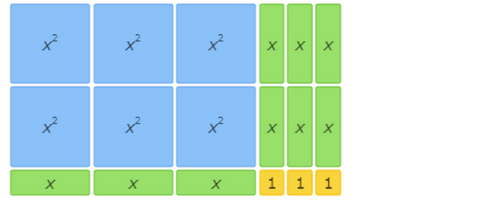
This area model shows 6x2+9x+3=(3x+3)(2x+1).
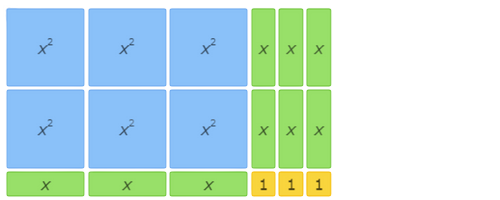
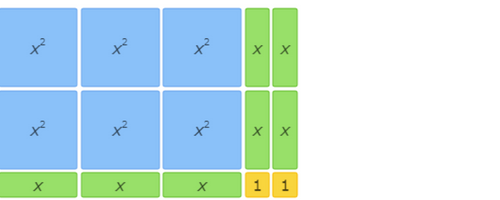
This area model shows 6x2+7x+2=(3x+2)(2x+1).
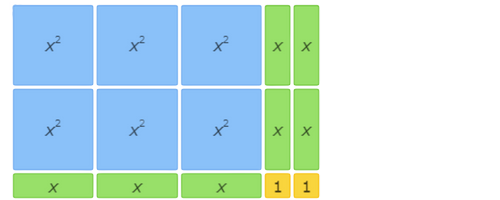
let’s practice!

