Look at the given quadratic:

y²+24y+23

The c term is 23, so you need to find a pair of factors with a product of 23. The b term is 24, so you need to find a pair of factors with a sum of 24. Since the product is positive (23) and the sum is positive (24), you need both factors to be positive.

Make a list of the possible factor pairs with a product of 23, and then find the one with a sum of 24.

The factors 1 and 23 have a sum of 24. Use those numbers to factorise y²+24y+23.

y²+24y+23

(y+1)(y+23)

Finally, check your work.

(y+1)(y+23)

y²+y+23y+23 Apply the distributive property (FOIL)

y²+24y+23

Yes, y²+24y+23=(y+1)(y+23).

Look at the given quadratic:

j²+24j+23

The c term is 23, so you need to find a pair of factors with a product of 23. The b term is 24, so you need to find a pair of factors with a sum of 24. Since the product is positive (23) and the sum is positive (24), you need both factors to be positive.

Make a list of the possible factor pairs with a product of 23, and then find the one with a sum of 24.

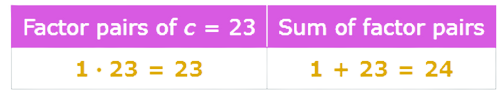
The factors 1 and 23 have a sum of 24. Use those numbers to factorise j²+24j+23.

j²+24j+23

(j+1)(j+23)

Finally, check your work.

(j+1)(j+23)

j2+j+23j+23Apply the distributive property (FOIL)

j²+24j+23

Yes, j²+24j+23=(j+1)(j+23).

Look at the given quadratic:

n2+6n+8

The c term is 8, so you need to find a pair of factors with a product of 8. The b term is 6, so you need to find a pair of factors with a sum of 6. Since the product is positive (8) and the sum is positive (6), you need both factors to be positive.

Make a list of the possible factor pairs with a product of 8, and then find the one with a sum of 6.

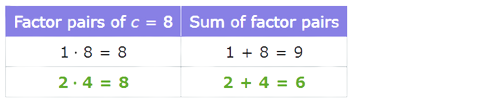
The factors 2 and 4 have a sum of 6. Use those numbers to factorise n2+6n+8.

n²+6n+8

(n+2)(n+4)

Finally, check your work.

(n+2)(n+4)

n²+2n+4n+8 Apply the distributive property (FOIL)

n²+6n+8

Yes, n²+6n+8=(n+2)(n+4).