Multiply two polynomials using algebra tiles
key notes:
- Understand Basic Algebra Tiles:
- Algebra tiles represent variables and constants visually. Typically, squares represent constants, and rectangles represent variables.
- Model Each Term:
- Break down each polynomial into its individual terms.
- Use tiles to model each term, considering the appropriate shape and size for variables and constants.
- Arrange Tiles for Each Polynomial:
- Lay out the tiles for one polynomial horizontally and the tiles for the other polynomial vertically.
- Multiply Each Pair of Tiles:
- Multiply each pair of tiles, considering both the numerical and variable components.
- For example, the product of a constant tile (square) and a variable tile (rectangle) is the product of their numerical coefficients and the product of their variables.
- Combine Like Terms:
- Combine the tiles with the same variable and exponent to simplify the expression.
- Arrange the tiles neatly to represent the final product.
- Count Tiles to Determine Coefficients:
- Count the number of tiles in each region to determine the coefficients of the terms in the final product.
- Illustrate the Distributive Property:
- Emphasize the connection between the visual model and the distributive property.
- Show how each term in one polynomial is multiplied by each term in the other polynomial.
- Practice with Examples:
- Work through several examples with different polynomials to reinforce the understanding of the process.
- Check the Result:
- Validate the final result by multiplying the polynomials using the traditional algebraic method to ensure consistency.
- Use Algebra Tiles as a Learning Tool:
- Encourage students to use algebra tiles as a tool to visualize and understand polynomial multiplication, especially when introducing the topic.
Learn with an example
Which multiplication expression does this area model represent?
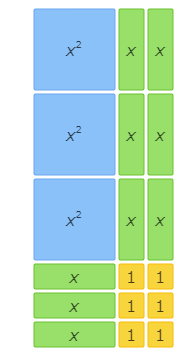
(x+2) (3x+3) (2x+2) (3x+3)
(x+1) (3x+3) (2x+3) (3x+3)
Look at the base. The base is made up of 1 x tile and 2 1 tiles. So, the base represents (x+2)
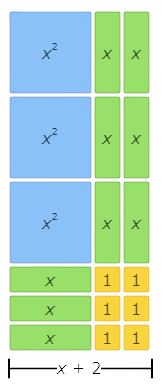
Next, look at the height. The height is made up of 3 x tiles and 3 1 tiles. So, the height represents (3x+3)
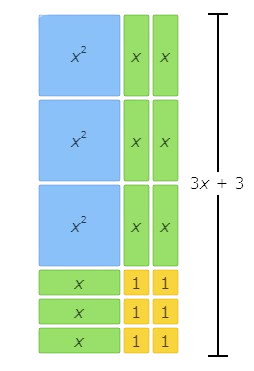
Finally, multiply the base and the height. This area model represents (x+2) (3x+3)
Which area model represents the expression (3x+1) (x+2)?
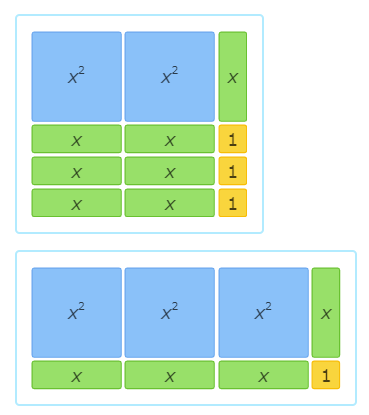
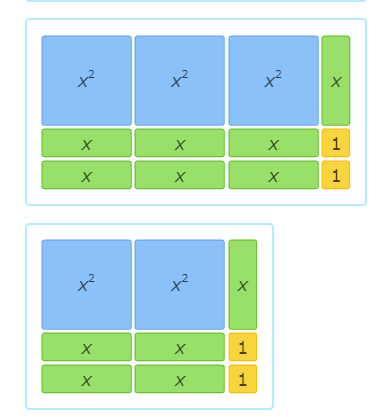
This is the area model that represents the expression (3x+1) (x+2)
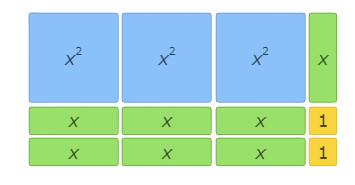
Look at the base. The base is made up of 3 x tiles and 1 1 tile. So, the base represents (3x+1)
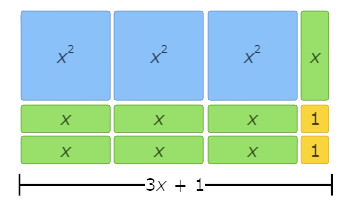
Next, look at the height. The height is made up of 1 x tile and 2 1 tiles. So, the height represents (x+2)
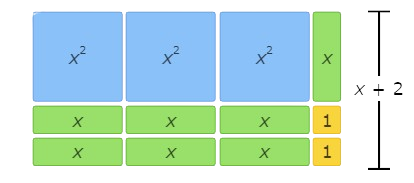
Finally, multiply the base and the height. This area model represents (3x+1)(x+2)
The other area models represent different expressions.
This area model represents(2x+1) (x+3)
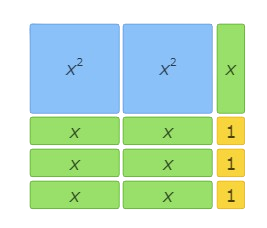
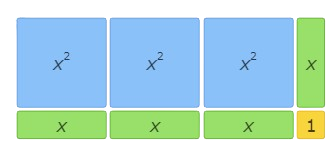
This area model represents (3x+1) (x+1)
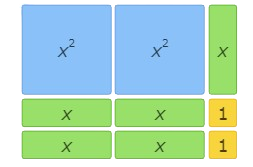
This area model represents(2x+1)(x+2)
let’s practice!🖊️

