Add polynomials to find the perimeter
key notes:
- Understanding Polynomials:
- A polynomial is an algebraic expression consisting of variables and coefficients, combined using addition, subtraction, and multiplication, but not division by a variable.
- Perimeter of Geometric Figures:
- Perimeter is the total length of the boundary of a geometric figure.
- For rectangles and squares, the perimeter is the sum of all four sides.
- Expressing Perimeter with Polynomials:
- Express the algebraic expressions representing the lengths of the sides of a geometric figure as polynomials.
- For example, if the length of a rectangle is represented by 2�+32x+3 and the width by �+2x+2, the perimeter is the sum of all four sides: 2(2�+3)+2(�+2)2(2x+3)+2(x+2).
- Combine Like Terms:
- Combine like terms within the polynomial expression to simplify it.
- In the example above, combine 2�2x and 2�2x to get 4�4x, and combine constants 33 and 22 to get 55.
- Finding the Final Perimeter:
- Once the polynomial expression is simplified, it represents the perimeter of the geometric figure in terms of the variable.
- Substitute specific values for the variable to find the numerical value of the perimeter.
- Examples:
- Work through examples involving rectangles, squares, or other geometric shapes where the lengths of the sides are represented by polynomial expressions.
- Practice combining like terms and finding the perimeter.
- Word Problems:
- Apply the concept to solve real-world word problems. For instance, find the perimeter of a rectangular garden given the algebraic expressions representing its dimensions.
- Review:
- Emphasize the importance of reviewing the steps: representing sides as polynomials, combining like terms, and simplifying to find the perimeter.
- Extension:
- Explore extending the concept to more complex shapes, such as irregular polygons, by breaking them into simpler shapes and applying the same principles.
- Practice:
- Provide ample opportunities for practice to reinforce the concept. Include a variety of shapes and expressions to ensure a comprehensive understanding.
Learn with an example
➡️ Find the perimeter.
Simplify your answer.

Add the side lengths.
v + 1 + v + 1
(v + v) + (1 + 1) Group like terms
2v + 2 Combine like terms
The perimeter is 2v + 2.
➡️ Find the perimeter.
Simplify your answer.
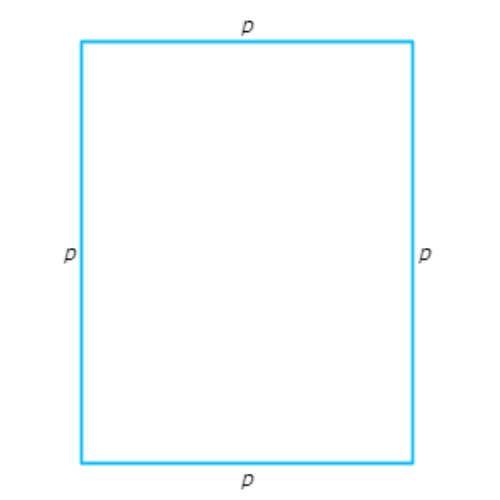
Add the side lengths.
p + p + p + p
4p Combine like terms
The perimeter is 4p.
➡️ Find the perimeter.
Simplify your answer.
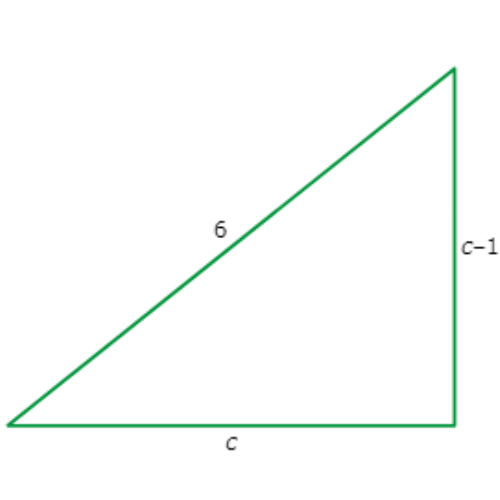
Add the side lengths.
6 + c + (c – 1)
(c + c) + (6 – 1) Group like terms
2c + 5 Combine like terms
The perimeter is 2c + 5.
let’s practice!🖊️

