Multiply two matrices
key notes:
To find the element in the ith row and jth column of the product of two matrices, multiply each element in the ith row of the first matrix by the corresponding element in the jth column of the second matrix. Then add the products.
Learn with an example
Fill in the missing number.
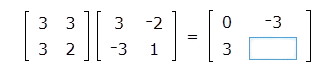
To remember how to multiply two matrices, first, imagine the two matrices with the second matrix moved up. Imagine the product of the two matrices sitting to the right of the first matrix and below the second matrix. The product will have the same number of rows as the first matrix and the same number of columns as the second matrix.
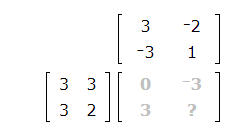
The blank is in row 2 and column 2. Locate row 2 of the first matrix and column 2 of the second matrix.
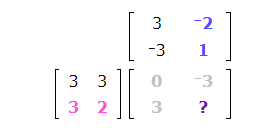
Pair the elements of row 2 of the first matrix with column 2 of the second matrix. To find the number that belongs in the blank, take the products of these pairs, and then take the sum of the products.
3(-2) + 2(1) = -4
Thenumber -4 belongsintheblank.
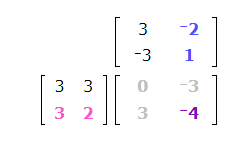
This is the product of the two matrices:

Fill in the missing number.
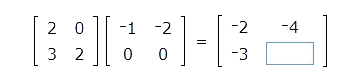
To remember how to multiply two matrices, first, imagine the two matrices with the second matrix moved up. Imagine the product of the two matrices sitting to the right of the first matrix and below the second matrix. The product will have the same number of rows as the first matrix and the same number of columns as the second matrix.
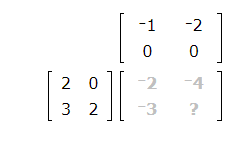
The blank is in row 2 and column 2. Locate row 2 of the first matrix and column 2 of the second matrix.
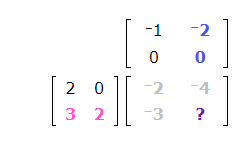
Pair the elements of row 2 of the first matrix with column 2 of the second matrix. To find the number that belongs in the blank, take the products of these pairs, and then take the sum of the products.
3(-2) + 2(0) = -6
The number -6 belongs in the blank.
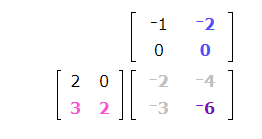
This is the product of the two matrices:
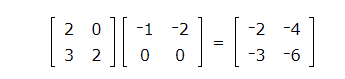
Fill in the missing number.
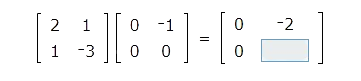
To remember how to multiply two matrices, first, imagine the two matrices with the second matrix moved up. Imagine the product of the two matrices sitting to the right of the first matrix and below the second matrix. The product will have the same number of rows as the first matrix and the same number of columns as the second matrix.
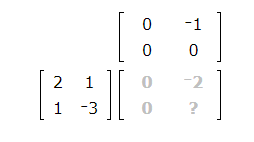
The blank is in row 2 and column 2. Locate row 2 of the first matrix and column 2 of the second matrix.
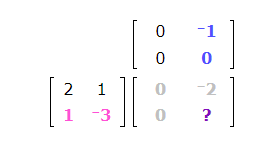
Pair the elements of row 2 of the first matrix with column 2 of the second matrix. To find the number that belongs in the blank, take the products of these pairs, and then take the sum of the products.
1(-1) + -3(0) = -1
The number -1 belongs in the blank.
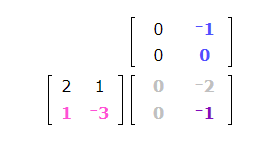
This is the product of the two matrices:
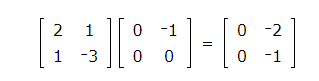
Let’s practice:

